Tyre Wear Model – Abstract
Tyre Wear Model – Wear is due to many causes and involves three major consequences: loss of performance, loss of security and environmental pollution. Depending on the context, the focus on the consequence can be moved: in motorsport tyre’s fundamental role is to guarantee high performance as long as it is possible, in road vehicles safety has decisive importance compared to the safety target, in big densely-populated cities the pollution due to tyre particles can be of considerable importance.
The main objective of this work is to describe a necessary set of instruments concerning tyre wear mechanism-related phenomena, allowing to better understand and to develop an improved formulation, able to consider the tread compound viscoelastic characteristics, the pavement roughness and the tyre operating conditions. To this purpose the modelling approach considers the viscoelastic behaviour of the compound, changing instant by instant its nominal characteristics as a function of the excitation frequency and the material temperature.
To validate the modelling approach proposed and its reliability in completely different scenarios of use, the authors have selected five datasets collected on vehicles belonging to diverse motorsport, passenger and truck categories, unique in terms of vehicle operating conditions both from kinematic-dynamic and thermodynamic points of view.
1. Introduction
Since the tyres represent the only interface between vehicles and road surfaces, from the design point of view, a compromise must be found between the different and often contrasting functional goals, such as (wet) braking, mileage, rolling resistance, and noise emission [1], [2]. In addition, due to their economic and ecological implications, wear particle emission comes more and more into the focus of legislative institutions [3], [4], [5]. Indeed, increasingly adopted electric and hybrid propulsion systems are expected, on one hand, to impact less in terms of direct engine-related emissions, but to be pointed out as an increased source of non-exhaust pollution related sources, such as tyre wear, due to their significantly increased mass, on the other [6], [7].
Typically, wear is related to sliding friction and quantified with the amount of the material removed, but different types of wear can be observed with the rate and extent of wear depending on different mechanical, physical, chemical and electrical phenomena possibly taking place either separately or at the same time. Several wear classification methods have been addressed and classified in the literature such as abrasion, adhesive wear, corrosion and surface fatigue wear [8], [9]. In the context of rubber wear, the problem is even more complicated. As concerns rubber compounds, such as tyres, further complications arise from the fact that polymers vary their properties as a function of material temperature and excitation frequency [10], [11]. A close relation between friction and wear in rubbers is given in [12], where the abrasion and roll formation are correlated with the adhesion friction, while the fatigue wear is linked to the hysteresis friction. In [13], besides the relation between friction and abrasion of rubber mentioned above, the phenomenon of waves of detachment existing on the rubber surface when sliding over a hard track, or vice versa, following adhesive effects and buckling of the rubber surface is identified as a feature of rubber abrasion. Later, in [14], the authors affirm that abrasion can be even not distinguishable from wear (words “wear” and “abrasion” are used alternatively, indeed) since abrasion is usually the most dominant mode of rubber wear, covering all the above wear mechanisms [15] especially for tyres, where the other mechanisms become relatively significant only if a long duration of sliding persists. Abrasive processes have been also investigated highlighting the importance of reproducing in laboratory tests similar conditions of rubber-rough surface dynamic contact experienced in a tyre footprint to study accurately wear phenomena [16]. The importance of the mean wavelength on the worn rubber surface as a good indicator of the wear rate has been proved along with the fact that the adhesion mechanism, estimated starting from the surface energies evaluation, is relevant for a more accurate investigation of friction phenomena [17]. Indeed, by focusing primarily on the rubber-surface interfacial behaviour rather than on the viscoelastic properties of the rubber material, the adhesion friction coefficient becomes the most dominant term in rubber friction analysis [18].
In this work, following the classification of wear mechanisms in [9], the authors do not consider the corrosive mechanism since the tyre and the road hardnesses are not similar. In the proposed approach the authors do not distinguish between the adhesive and hysteretic contributions since the forces, responsible for the friction generation mechanisms, are considered as a whole as the model input; the viscoelastic properties of the material are evaluated moment by moment taking into account the instantaneous boundary conditions. In these hypotheses, the fatigue wear concept [19], relying on a process occurring in a material subjected to cyclic stresses and strains at high-stress concentration locations and where wear particles are generated by fatigue-propagated cracks, is proposed as wear abrasion or simply wear.
The proposed wear model originates as an evolution of the models in the literature with special attention to the influence that the tyre temperature has on the wear phenomenon. The aim of this work is to provide a holistic simulation tool for tyre wear prediction, able to take into account tread rubber characteristics, road surface properties, thermal effects and tyre operating conditions, in their turn depending on a given dynamic scenario. To this end, the strong temperature dependence has been taken into account by coupling the stress-state-dependent damage model used in the wear formulation with a thermal solver.
In literature, the wear rate of tyre tread is often described by a function proportional to the frictional power dissipated during contact, while the frictional power is directly dependent on the local sliding speed, the local contact pressure, and the coefficient of dynamic friction [20], [21]. However, these parameters are a direct consequence not only of the tyre construction and the manoeuvres in which the tyre undergoes [22], [23] but also of the road characteristics and boundary conditions as the temperature, pressure and velocity distributions within instantaneous contact patch, kinematic and dynamic quantities transmitted via tyre tread and materials’ properties in mutual contact [24], [25]. The necessity to shift the paradigm and to formulate the tyre wear model from a multidisciplinary perspective has been first pointed out in [26], where an impressive experimental campaign has been conducted to quantify potential thermal, degradation and material influences. Although these existing models, which are mostly dependent on contact pressure and sliding velocity, can be used to determine the material loss of a particular wear mechanism, they cannot describe the history of the abrasion process taking into account the thermodynamic history of the material. The effects of the tread thickness material removal on the vehicle frictional performance and the tyre thermodynamic behaviour have been already analysed in [27] and, recently, in [28], [29] an optimal control for the management of the tyre performance has been formulated as a function of temperature and wear phenomena, showing interesting potential in the ability to govern the grip during the extended tyre life. Furthermore, the scientific community completely agrees that the wear phenomenon is local, the function of the local pressure, temperature and velocity distributions within the contact patch which are not so easy to obtain [30], [31], [32], being currently not directly measurable in the real road scenario [33], [34], [35], and whose determination usually relies on mathematical formulations, frequently involving nonlinear finite element analysis, brush theories, and flexible multibody-based approaches [36], [37]. In addition, the evaluation of the compound characteristics is usually evaluated through destructive approaches, forcing the prototyping engineers to feed the preliminary models with nominal, and not usually reliable, viscoelastic data [38], [39].
The proposed methodology starts from the accurate modelling of the different above-mentioned involved aspects, linking them in a comprehensive predictive instrument. To validate the proposed physical formulation in a wide working range, a specifically-selected experimental dataset has been carried out. It includes industrial partners’ and research laboratory’s tyre data, comprehending four different tyre compounds and corresponding vehicle setups.
The paper is organized as follows: in Section 2, the studies concerning the material viscoelastic modelling, the time-temperature superposition effect, the tyre thermal model as well as the road conditions and contact mechanics are discussed; in Section 3 the material damage and the resulting wear formulation are illustrated; in Section 4, the experimental data, employed as an experimental reference dataset for the study, demonstrating the model reliability to reproduce the material removal for different tyres and in diverse thermal and dynamic operating conditions are described; in Section 5, an additional discussion on results and further model employment are proposed.
2. Multidisciplinary approach
The dynamic characteristics of a tyre can vary greatly during its motion due to its internal structure-linked interactions between different materials and the peculiar viscoelastic properties of the rubber matrix [40], [41]. Factors such as inner pressure, temperature, pavement granularity, and others can all have an impact [42]. To accurately analyse and model a tyre’s behaviour, a multi-physical approach is necessary, taking into account the effects of temperature on the structural and viscoelastic properties of the tyre, as well as the effects of speed and road surface roughness. Indeed, among the physical aspects to be considered for an accurate mathematical representation of the wear mechanism, the effect of the extremely fast surface temperature arising at the compound-road interface [43], road roughness characteristics [44], hysteretical transient-driven effects [45], time-temperature superposition principle [46], and eventual material degradation process [47] should be at least considered.
The functional scheme of the modelling approach is proposed in Fig. 1. Starting from the relative velocity defined at the contact patch and the road roughness characteristics expressed in terms of macro parallel 𝜉∥ (m) and perpendicular 𝜉⊥ (m) correlation lengths the excitation frequency 𝑓 (Hz) is defined (Section 2.3). The instantaneous viscoelastic properties, expressed in terms of storage modulus ∇𝐸′ (Pa) and loss factor ∇tan𝛿 (-) per each node, are obtained employing the temperature distribution input ∇𝑇 (K), available as an output from a properly calibrated tyre thermal model [48], and the excitation frequency 𝑓 from the compound master curve data and applying the time-temperature superposition principle [49] (Sections 2.1 Compound viscoelasticity and TTS principle, 2.2 Compound thermodynamics). Furthermore, the same quantities ∇𝑇 and 𝑓 are further employed to extract the ∇𝑆−𝑁 damage curves per each node for the same instantaneous operating conditions, which will feed the damage accumulation formulation of the damage block. The generalized force 𝐹→={𝐹𝑥,𝐹𝑦,𝐹𝑧} (N) defined at the contact patch and the viscoelastic properties ∇𝐸′ and ∇tan𝛿 defined per each node feed the contact mechanics block where the indentation levels and the stress–strain distributions are computed in run time [27], from which the equivalent stress ∇𝜎𝑒𝑞 is evaluated per each node (Section 2.4). Finally, the damage ∇𝐷 is cumulated employing the Miner’s methodology [50] using the instantaneous 𝑆−𝑁 curves, depending on the actual temperature conditions ∇𝑇 of each node and the excitation frequency 𝑓, according to which the material removal depends on the damage level achieved within the tread compound thickness (Section 3).
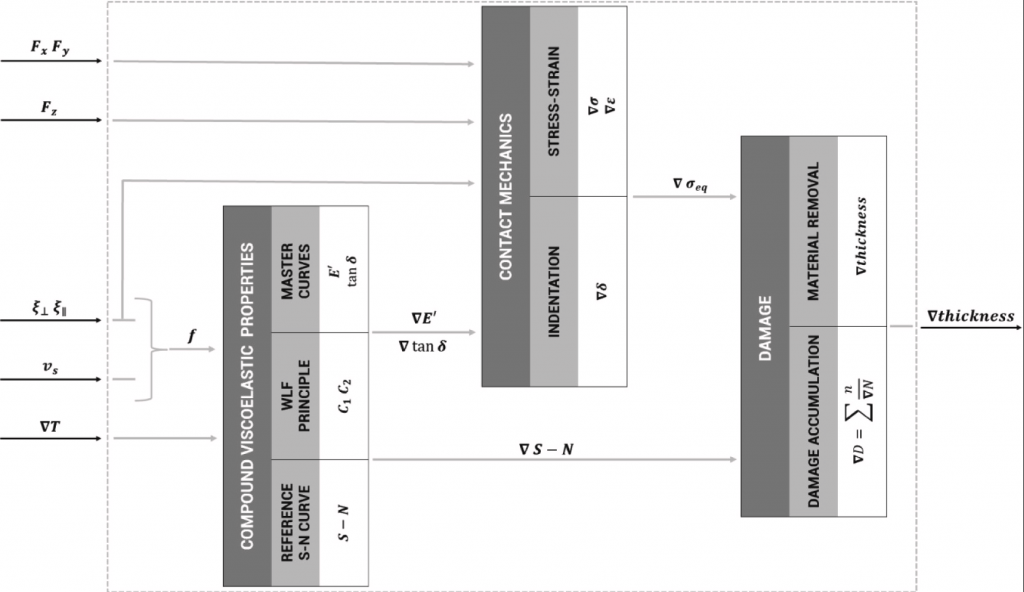
Fig. 1. Model functional scheme.
It is worth highlighting that the wear model is fed by the instantaneous forces in input, but it also affects the tyre mechanical characteristics since both stiffness and adherence factor are influenced by the amount of hysteretical energy dissipated within the compound-pavement interaction, as described in [27], [51]. For this reason, even if this work only addresses the wear modelling approach, the wear model itself has to be imagined as one of the co-simulated modules each contributing to the description of the tyre-road interaction: thermodynamics, wear mechanics, adherence module and kinematic-dynamic wheel hub-contact patch module [36], [51].
2.1. Compound viscoelasticity and TTS principle
The capability to accurately represent the viscoelastic properties of a material is crucial for obtaining reliable results from analytical models or finite-element-based analyses [52]. Viscoelastic materials have both elastic and viscous properties, relying on an intrinsic rheological stress–strain dependence on time [53], and their dynamic behaviour is represented by a complex variable 𝐸∗, which defines the dynamic stiffness:
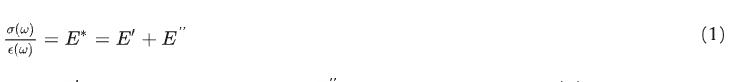
where 𝐸′ is the storage modulus (Pa), 𝐸′′ is the loss modulus (Pa), 𝜎(𝜔) is the cyclic stress applied to the material (Pa) at given angular frequency 𝜔=2𝜋𝑓 (Hz), and 𝜖(𝜔) is the corresponding strain response (-).
The hysteretical behaviour is deeply linked to the phase angle tan(𝛿), or also loss factor, expressed as:

It is important to note that the physical quantities 𝐸′, 𝐸′′, and tan(𝛿) defined in (1) and (2) are dependent on the frequency at which a harmonic load-deformation is applied on the material at a specific temperature. To extend the material’s properties over a broader frequency or temperature range, which is important for applications such as contact, friction, and wear modelling, the time-temperature superposition (TTS) is applied [49], [54]. The frequency-temperature superposition principle relates the material response at a given time 𝑇 (or angular frequency 𝜔), and at a given temperature 𝑇, to that at other conditions (denoted by subscript 𝑟):

where 𝑎𝑇(𝑇,𝑇𝑟) and 𝑏𝑇(𝑇,𝑇𝑟) are coefficients representing horizontal and vertical shifts respectively to be applied to isotherms of storage and loss moduli measured at a temperature 𝑇 in order to estimate the material properties at a reference temperature 𝑇𝑟, with 𝑎𝑇(𝑇,𝑇𝑟) describing the temperature dependence of the relaxation time, usually following the empirical Williams-Landel-Ferry (WLF) law (4)[49]

where 𝐶1 and 𝐶2 are empirical constants whose order of magnitude is about 10 (-) and 100 (K), respectively. The hypothesis concerning the vertical shift factor 𝑏𝑇(𝑇,𝑇𝑟), related to thermal expansion effects, which for most polymers (and in this work) can be neglected due to their small variation, is highly acceptable in the viscoelastic regions where the frequency/time dependence of material functions is sharp.
To analytically describe the mechanical behaviour of the viscoelastic material over a vast range of excitation frequencies using a limited number of parameters with acceptable accuracy, the authors have effectively applied fractional models [55], whose constitutive equation is based on fractional derivative orders:

where 𝛼𝑛 and 𝛽𝑚 are the fractional derivative orders included within the range [0,1], 𝑁=𝑀 and 𝑏0=0 for the considered Maxwell formulation. Turning to the frequency domain by applying the Fourier transform and assuming that 𝛼=𝛽, Eq. (5) provides an even more useful expression of complex modulus(6), which can be employed in the mathematical description of the viscoelastic material in the wear model:

where the parameters 𝐸𝑘 and 𝜂𝑘 represent the discrete spring stiffness and spring-pot coefficients of the Maxwell model [55], respectively, and 𝜔 is the angular excitation frequency. It is worth pointing out that the described analytical approach results particularly effective to evaluate the material’s viscoelastic characteristics as the number of nodes could grow (i.e. in finite-element analysis techniques) since it completely avoids initializing pre-discretized frequency and temperature ranges and therefore preserves both memory management and run-time performance.
2.2. Compound thermodynamics
To describe the complexity of transient thermodynamic phenomena under investigation, the authors have designed a computationally efficient tyre thermodynamic model based on the Fourier heat transfer principle [48], able to accurately reproduce the temperature gradient of the extremely non-linear tyre system, in all possible operating conditions of interest [51].
Each layer of the tyre has been modelled within a three-dimensional heterogeneous domain and the power balance equation on heat transfers has been formulated for each node:
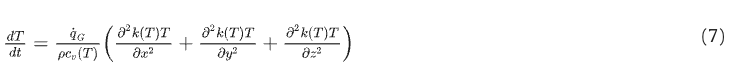
where the diffusivity parameters, i.e. density 𝜌, conductivity 𝑘 and specific heat 𝑐𝑣, depend on the node position 𝑥,𝑦,𝑧 within the tyre threedimensional domain and its instantaneous temperature state 𝑇. Two main sources have been taken into account to calculate the heat generation factor: the first contribution, related to the asymmetrical pressure distribution in the rubber-road contact region together with continuous loading-unloading cycles, causes a progressive energy loss due to hysteretic behaviour of the rubber; the second one, on the other hand, is linked to the heat generated from sliding friction. The system boundary conditions, i.e. road 𝑇𝑟𝑜𝑎𝑑 and air 𝑇𝑎𝑖𝑟 temperatures taking into account the track conditions and vehicle characteristics (geometry, suspension characteristics, etc.), as well as the eventual presence of additional heating (brakes) and cooling (diffusers) sources, distinguish different vehicle setups and weather conditions.
The three-dimensional temperature gradient ∇𝑇, concerning the tread compound layer, is then adopted together with the knowledge of the instantaneous excitation frequency 𝑓, described in Section 2.3, within the determination of the stress and strain state within the rubber material, making use of the time-temperature superposition principle. The thermal state information is particularly relevant for a reliable study of the wear phenomenon since it considers not only the temperature measures acquirable on the internal and external surfaces of the tyre tread but also the ones concerning the gradient ∇𝑇 within the material thickness, significantly affecting the material viscoelastic characteristics and therefore the strain–stress distributions ∇𝜎 and ∇𝜖 levels of the entire tread rubber block.
2.3. Road profile and instantaneous operating conditions
Surface roughness refers to variations in height relative to a reference plane and is usually measured along a single line or a set of parallel line profiles (surface maps), starting from which typically two post-processing stages are performed to evaluate the surface characteristics: levelling the profile to remove the potential underlying inclination and applying a filter [56].
Once the primary profile has been levelled and the offset and slope suppressed, different statistical height descriptors or spectral analysis techniques can be employed to synthesize the road roughness characteristics [57].
The wear model is based on contact mechanics, relying on the mathematical description of the contact between a set of equally-spaced rigid indenters, representing the road roughness characteristics, and a semi-space of a known elasticity, representing the tyre compound [43]. A schematic representation of the mathematical description of the mutual contact between the road-representative indenters and the rubber-representative elastic semi-space is illustrated in Fig. 2. The indenters’ geometry and spacing within the tyre–road contact patch are defined starting from the road data macro wavelength, obtained by means of the power spectrum density technique [57], where the quantities 𝜉∥ (m) and 𝜉⊥ (m) define the parallel and the perpendicular correlation lengths relative to the macro-wavelength, respectively.
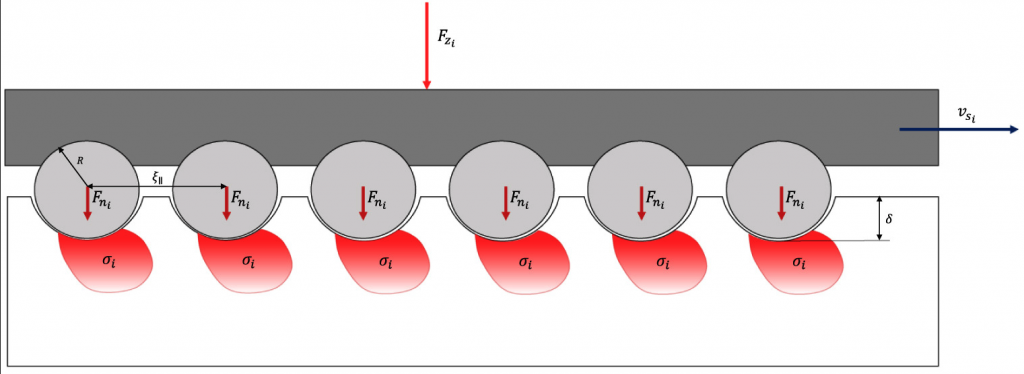
Fig. 2. Rigid indenters and elastic semi-space contact.
The indenters’ geometry and spacing, once initialized as a function of the road roughness properties in terms of 𝜉∥ and 𝜉⊥, are then employed to evaluate the material excitation frequency 𝑓 (Hz), as follows:(8)𝑓=𝑣𝑠𝜉∥which is necessary, together with the temperature gradient ∇𝑇, for the determination of the instantaneous viscoelastic characteristics in terms of ∇𝐸′ and ∇tan𝛿. Furthermore, as illustrated in Fig. 1, Fig. 2 and explained in Section 2.4, the indenters are further employed in the evaluation of the instantaneous indentation levels 𝛿 (m) and stress–strain states ∇𝜎 (Pa) and ∇𝜖 under the boundary conditions in analysis, expressed in terms of local friction coefficient and local pressure.
2.4. Contact mechanics
To theorize the contact between rough surfaces, different studies [43], [58], [59], [60], [61] have been conducted. To determine the interior stress field for the case of two bodies elastically dissimilar, with the half-space elastic body indented by an axisymmetric indenter sliding along and developing a frictional force, the research outputs from [62], [63] have been adopted for the current study. In particular, the technique, based on the knowledge of the normal displacement of the surface due to shearing tractions, is supposed proportional at each point to the contact pressure, starting from the theory of potentials [64].
The mathematical model for the indentation 𝛿 is based on the approximate viscoelastic solution obtained in [65], relying on the demonstration that the material relaxation response to the strain increment is significantly faster that the creep response to a stress increment:

where 𝛿𝐻 is the Hertzian indentation [66], 𝑇 is the material relaxation time constant and 𝜔 (rad/s) is the angular frequency relating to the normal load variation, supposed by the authors for simplicity equal to the wheel’s rotating velocity.
The indentation level 𝛿 for each asperity has been employed within the definition of the harmonic potential 𝜓, as described in [63], [67], so that the stress of state of each node of the elastic semi-space induced by shear traction in the 𝑥−, 𝑦− and 𝑧− directions can be evaluated as follows:
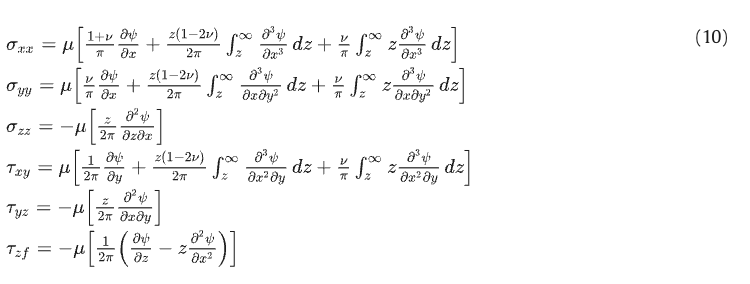
where 𝜓 is a harmonic potential defined for the case of normal loading alone in case of sliding plane contacts [63], neglecting the possible influence of the frictional shear on normal surface displacement. Furthermore, since the indentors could potentially assume any dimension (depending on the macro wavelength quantity referring to the road roughness characteristics), the authors have added the linear superposition hypothesis to the proposed formulation, originally formulated for a single indenter and an infinite elastic semi-space, to extend the applicability of the equation set (10) to an equally distributed set of indentors with representative dimensions 𝜉∥ and 𝜉⊥.
An example of the application of the implemented contact mechanics theory is proposed in Fig. 3, where components of the stress state along the radial direction 𝜎𝑧, 𝜏𝑦𝑧 and 𝜏𝑥𝑧, i.e. along the thickness of the tyre tread, are represented.
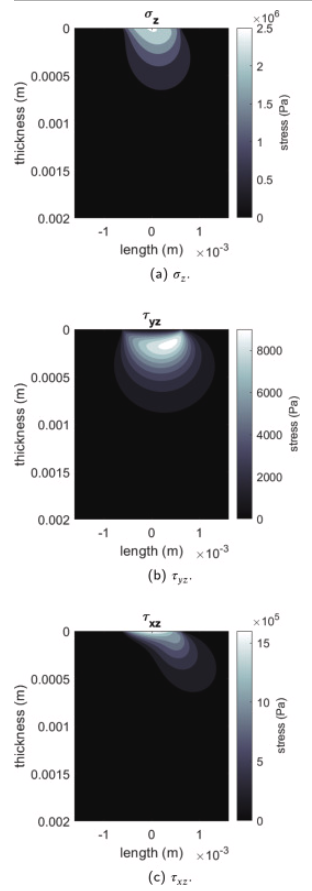
Fig. 3. Trend in the radial direction of some elements of the stress state induced by the plane indenter contact.
3. Modelling of the wear mechanism
The local contacts between asperities and elastic semi-space accompanied by very high local stresses are repeated a large number of times in the course of sliding or rolling, so governing the damage accumulation mechanism.
Starting from Miner’s [50] heuristic linear rule of cumulative damage [68], describing the fatigue of elastic structures under cyclic loading varying in time, additional complexities have to be addressed in order to tackle the fatigue in polymer materials due to the fact that both stress and strain are time-shifted. Considering the tread rubber control volume, the damage of an elementary volume of material due to fatigue can be described through a constitutive variable 𝐷 lying in the interval (0,1), which reduces the specific free energy by the factor 1−𝐷, or 1−𝐷𝛼 in case of elastomers [69]:

where 𝑁𝑓=𝑁𝑓(𝐶) denotes the number of cycles at the failure of the elementary volume, depending on the current load cycle 𝐶. Several works have deeply investigated the applicability of Miner’s linear damage rule to elastomeric materials. In [70]fatigue life analysis has been carried out on NR and SBR samples proving that Miner’s linear rule is a reasonable approach for fatigue life prediction under specific signals tested in the work. In [71], [72], [73], the authors have demonstrated the applicability of the Miner’s linear law of cumulative damage to elastomers, proposing generalized evolution laws, in which the derivative of damage can be expressed as a non-factorizable function of the instantaneous cyclic load and the damage itself. However, these approaches underly the introduction of additional heuristic coefficients, usually not easy to determine. In fact, another straightforward possible approach is proposed in this work, relying on the time-temperature superposition theory[49] applied to the Miner’s linear law [50]. In these hypotheses, Eq. (11) becomes a function of the material-related WLF coefficients 𝐶1 and 𝐶2, defining the Wohler curve for each couple of boundary conditions, expressed in terms of the volume temperature 𝑇 (K) and excitation frequency 𝑓 (Hz):

which can be easily extended to the entire discretized tyre tread volume, simply substituting the temperature ∇𝑇 distributions instead of single value node temperature 𝑇. For the sake of completeness, the necessary three-dimensional temperature distribution ∇𝑇 has evaluated employing the outputs of the co-simulated tyre thermal model [48], [51], and 𝑓 is the frequency induced by the macro-wavelength of the road profile for the instantaneous sliding velocity condition, defined in Eq. (8). For this reason, the cumulated damage for a selected material volume, resulting from a series of non-identical cycles 𝑁 with a different history of temperature 𝑇 and frequency 𝑓 level (i.e. different values of 𝑁𝑓(𝑇,𝑓)), can be defined as:

Once the elementary volume has reached the ultimate damage condition 𝐷=1, the underlying material is considered detached from the tyre tread and the adjacent node becomes the new contact node for the evaluation of stresses and strains, defined in the contact mechanics section, for the next simulation step.
4. Results and discussion
In order to validate the proposed tyre wear formulation, five types of tyres covering a wide range of applications and performance levels have been specifically selected. Analogous studies available in literature usually empirically rely on restricted experimental data, generally accessing the goodness of the model behaviour towards a limited working range, in terms of the interface temperature, road characteristics or rubber materials adopted [20], [21]. To overcome these intrinsic weaknesses, a heterogeneous dataset, comprehending data from different outdoor experimental sessions carried out with vehicles from diverse categories, including both high-performance cars and heavy-duty trucks, on asphalts of peculiar characteristics, was prepared [74], [75]. Indeed, demonstrating the proposed formulation’s generality and applicability, the authors aim to provide a simulation tool which could be included in the development of the vehicle onboard advanced control and monitoring systems able to take into account the physical phenomena involving tyre wear, therefore, improving the systems’ efficiency and reducing their environmental impact, as explained in [29], [36] where the tyre thermodynamics estimation and its impact on the system’s characteristics (friction and stiffness properties) were considered. The formulation, indeed, considers different kinematic, dynamic and thermal operating ranges, as well as, different tyre structures and compound viscoelastic characteristics, which, in turn, differently respond to various kinematic and dynamic inputs (Fig. 1), peculiar of single vehicles, and therefore influence the tyre wear [41].
For the sake of completeness, the main differences concerning the selected dataset are described in the following and summarized in Table 1. The viscoelastic master curves of the five compounds are depicted Fig. 4, while the corresponding road characteristics are shown in Fig. 5. The variability in terms of the viscoelastic properties of each compound in terms of the storage modulus 𝐸′, applying the time-temperature superposition principle over the range of frequencies (1–1000 Hz), is represented in Fig. 6.
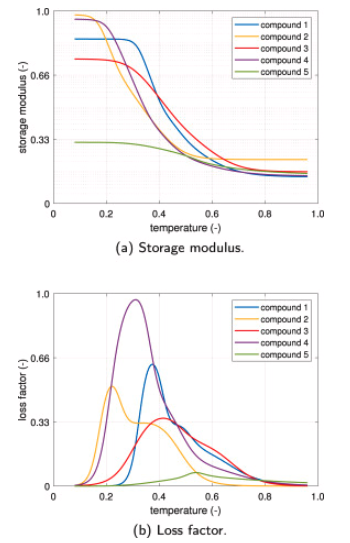
Fig. 4. Viscoelastic properties of the compounds evaluated by non-destructive VESevo technology [39].
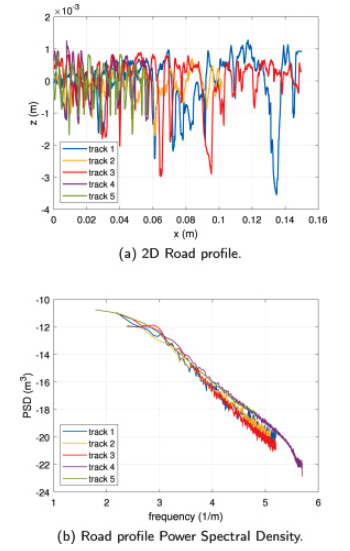
Fig. 5. Road texture 2D profile and PSD elaboration.
Table 1. Summary of the main characteristics of the datasets employed for wear formulation validation.
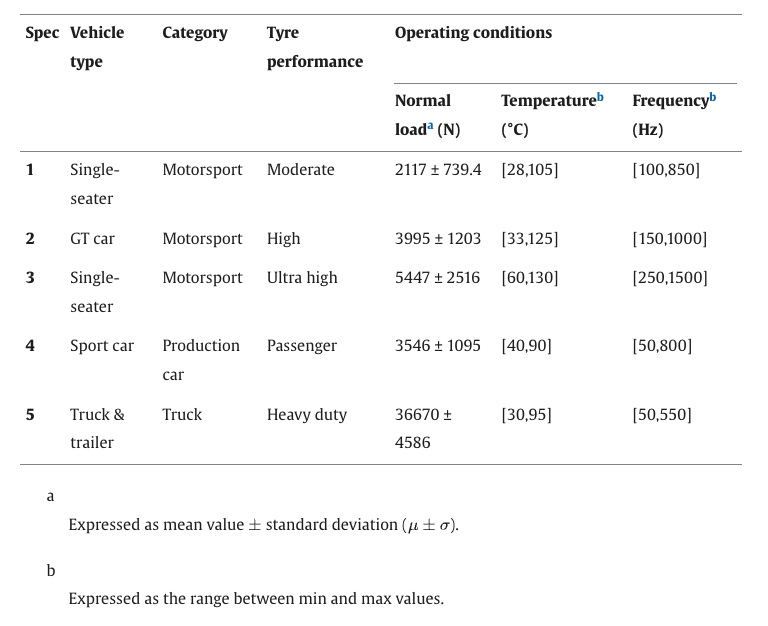
Due to confidentiality, only the main specifications concerning the tyre/vehicle category and the average operating conditions are reported for each tyre spec tested to validate the proposed modelling approach, and the data are non-dimensional in all figures, with reference to the same maximum values per each physical quantity concerning each tyre (storage modulus, loss factor, temperature):
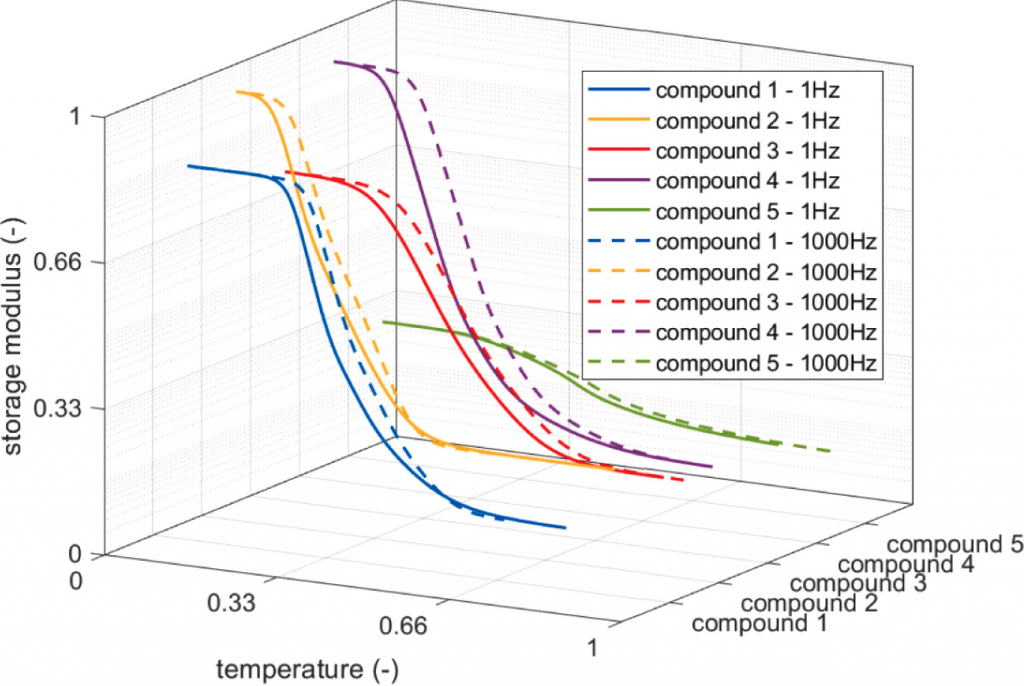
Fig. 6. Time-temperature superposition application.
compound 1
The tyre is used in motorsport competitions on single-seater vehicles characterized by low aerodynamic load and tread temperatures between 25 ° C and 105 ° C. Given the nature of the tracks and the rather low sliding speeds compared to other categories, the stress frequencies due to the road are between 100 Hz and 850 Hz. For this specific type of compound, six different runs have been collected with peculiar boundary conditions in terms of atmospheric temperatures fluctuating between 15 ° C and 30 ° C and asphalt temperatures between 18 ° C and 42 ° C;
compound 2
The compound is used to equip GT cars in motorsport competitions. The tyre is high-performance and is subject to significant normal loads. In this case, the stress frequencies are significantly higher, between 150 Hz and 1000 Hz, while the tread easily reaches temperatures of 30 ° C and 125 ° C. Two consecutive runs with similar thermal boundary conditions have been collected in the same test session: the first was between 23 ° C and 25 ° C while the second between 32 ° C and 35 ° C, for the outside air and asphalt temperatures, respectively;
compound 3
It is a high-performance slick tyre fitted on single-seaters with a high aerodynamic load. The slip rates to which it is subjected are very high, causing the highest stress frequencies in the entire dataset between 250 Hz and 1500 Hz. The tread reaches temperatures between 60 ° C and 130 ° C;
compound 4
The fourth tyre in the selected dataset is equipped for the production cars. It is a fairly sporty passenger tyre that is subjected to moderate normal loads, but due to its non-high performance, as it is not used in motorsport competitions, the stress frequencies are among the lowest of the entire dataset and the operating temperatures are between 40 ° C and 90 ° C. There are two runs selected for this type of tyre, with the same atmospheric conditions: air temperature of 25 ° C and track temperature of 42 ° C;
compound 5
The last tyre in the dataset is instead used on heavy-duty truck vehicles. It is subjected to the highest loads of the dataset, up to over 60 kN, with frequencies reaching values below 600 Hz given the low slips ratios to which it is subjected. The examined run consists of a pure rolling section lasting 12,000 s and a dynamic platform section of 2000 s in which the highest surface temperatures of the run are reached, about 90 ° C. The environment temperature is around 35 ° C with asphalt temperature reaching 50 ° C at the end of the run.
Starting from the observations of the previous study [27] concerning the wear influence on the tyre thermal dynamics, the authors have parameterized the tyre thermal model [48] able to provide tyre temperature local distributions, validating the instantaneous temperatures of the internal and external tyre layers, as shown in Fig. 7. It has to be highlighted that, even though it is clear that an eventually reduced tread thickness affects the rate of the hysteretical generative term within the dissipative tread volume, in the preliminary thermal calibration proposed in Fig. 8 the wear level is supposed constant for the entire simulation. The typical thermal trend consists of a first transient warm-up phase and a consequent thermal steady-state condition, usually kept until the wear phenomena become consistent, or the driving style changes significantly.
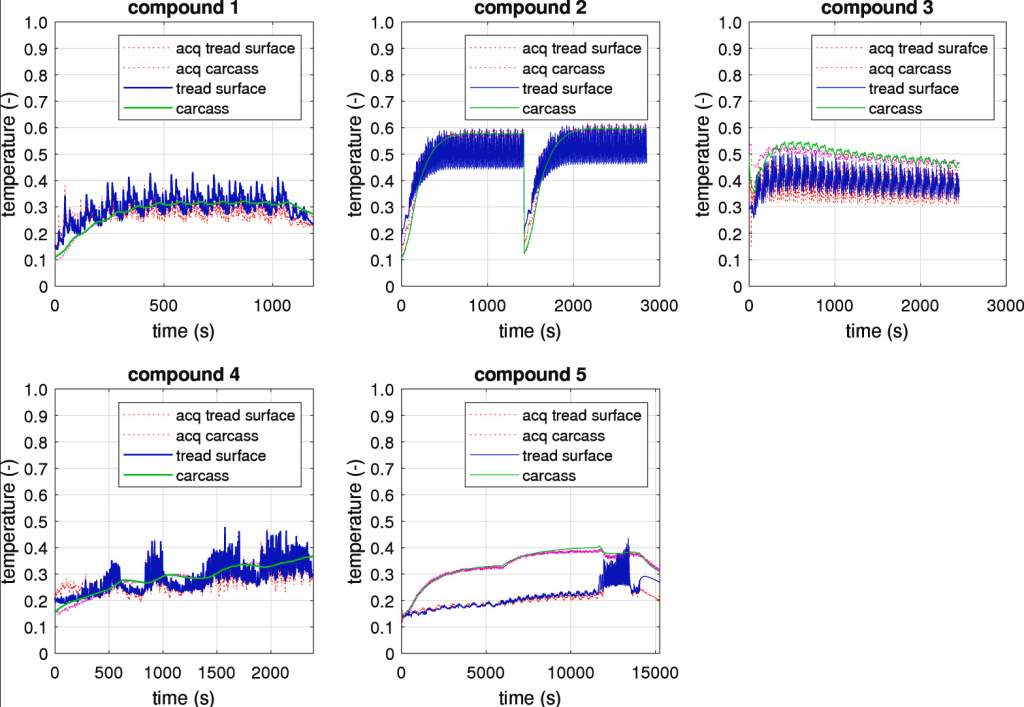
Fig. 7. Simulated vs experimental tyre temperatures.
Considering both the tyre radial and tangential temperature distributions, the radial gradient is further interpolated starting from the thermal model discrete outputs to enable the viscoelastic properties continuity within the compound bulk [41], while the tangential mesh is assumed the same for both thermal and wear models [48].
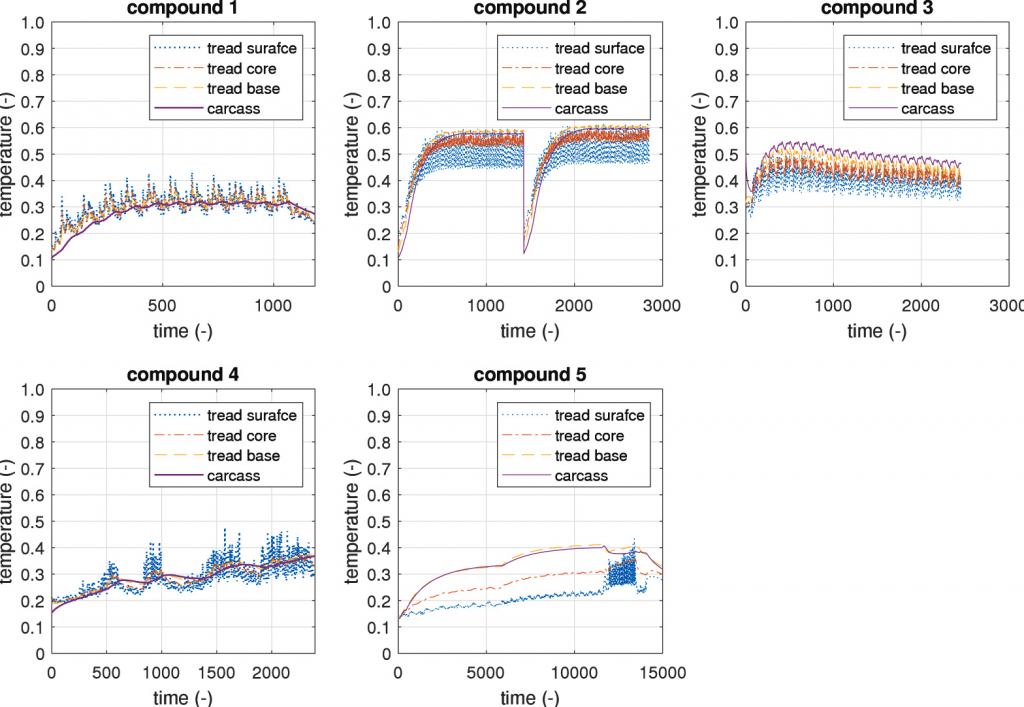
Fig. 8. Simulated tyre temperature gradients.
To effectively demonstrate how the instantaneous compound’s viscoelastic properties varied with frequency through the runs, the results of the time-temperature superposition principle applied to the master curves, originally presented in Fig. 4, are depicted in Fig. 9(a). Particularizing the shifted curves for specific temperature conditions explored by the tyres’ compounds (Fig. 8), it can be easily observed in Fig. 9(b) how the storage modulus 𝐸′ changed during the run, affecting other contact mechanics-related phenomena arising at the tyre–road interface. The most noticeable differences concern the heavy-duty truck spec 5 whose viscoelastic properties varied significantly between free-rolling and dynamic conditions, because of the different frequencies involved in these two cases due to the specific kinematic and dynamic operating conditions of the vehicle and tyres.
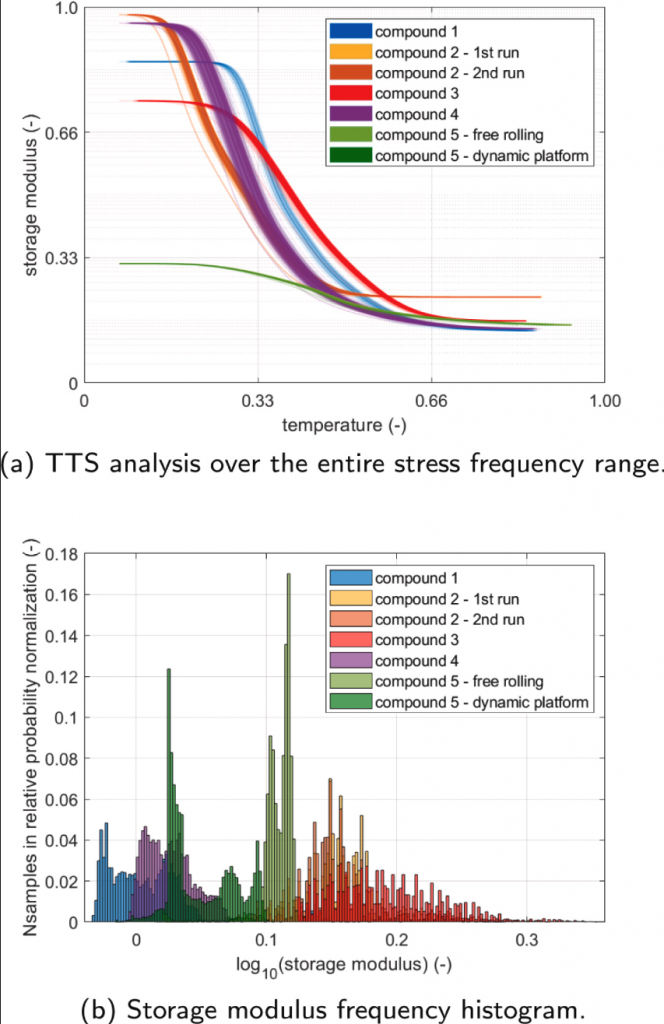
Fig. 9. TTS analysis and storage modulus frequency histogram based on corresponding telemetry data.
The stress-number of cycles relationship defined for each tyre in the dataset is shown in Fig. 10. This relationship is highly variable depending on the temperature variation of the material and the frequency to which it is subjected as depicted in Fig. 9. This results in a bundle of straight lines that identify the variable damage limit for a viscoelastic material as operating conditions vary (i.e. different values of 𝑁𝑓(𝑇,𝑓), as described at the end of Section 3). The observed intrinsic linear relationship between the stress state and the number of cycles is a direct expression of the viscoelastic material characteristics [27], [63]. In particular, the slope is closely related to the hardness and elongation in glassy conditions: in particular, in fatigue behaviour in a low-cyclicity context, thus influencing the value of 𝑁𝑓(𝑇,𝑓) [69]. Indeed, the relationship is not only dependent on the intrinsic characteristics of the material proposed by the previous studies discussed in Section 3, but it also varies in terms of temperature and frequency, as illustrated in Fig. 10, shifting the formulated linear function [51].
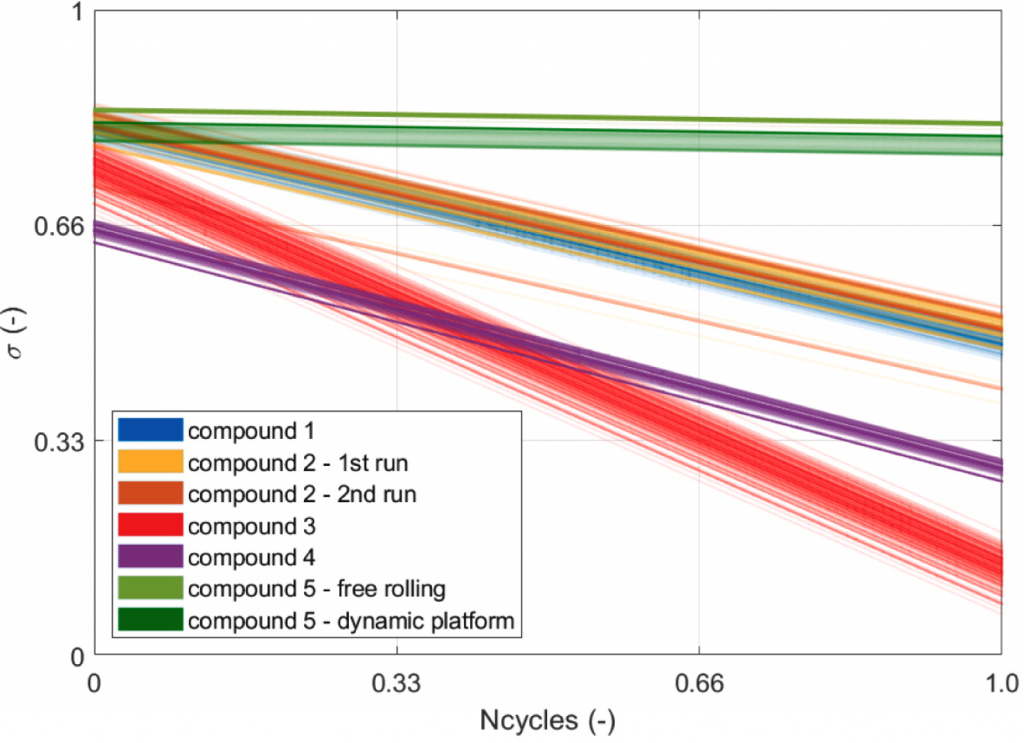
Fig. 10. Stress – number of cycles variation over the entire stress frequency range.
It is worth pointing out that the compound characteristics, as well as tyre geometry, could change with the mileage (i.e., with the tyre wear), affecting the contact mechanics and therefore the inputs of the wear model. In the present study, this update was considered only within the co-simulated thermal model as mentioned within the paragraph concerning the thermodynamic calibration, hypothesizing the kinematics, dynamics and contact patch size and shape evaluated at the nominal tyre properties.
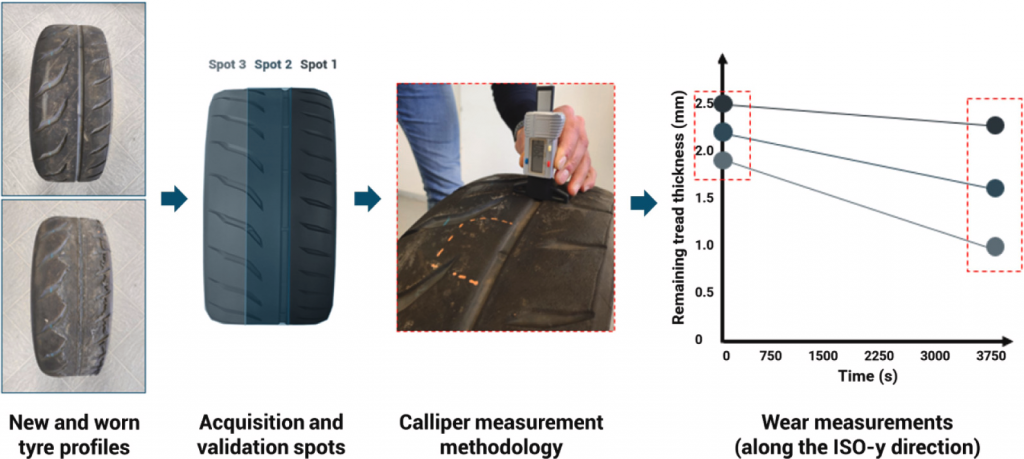
Fig. 11. Wear measurement scheme per tyre.
The experimental data were collected performing at least two measurements per dataset: the initial and final tread thickness values have been acquired by means of a calliper following the gauging scheme described in Fig. 11. The remaining thickness trends of all the ribs, corresponding to the acquired measurement spots (from 1 to 3 per each tyre), discretized within the wear model along the lateral ISO-y direction are represented in Fig. 12, where each colour represents a specific vehicle with its own set of tyres operating on a precise road surface, starting from peculiar tyre thermodynamic and weather conditions. It is worth mentioning that only one tyre per vehicle has been represented even if the validation has regarded 2 tyres per vehicle (front (steering) axle has been chosen since in the measurement campaign the removed thickness levels were more observable). Furthermore, each simulation not only regards a specific vehicle with peculiar kinematic-dynamic and thermal states, but it also takes into account specific road profile characteristics, reported in Fig. 5 per each dataset.
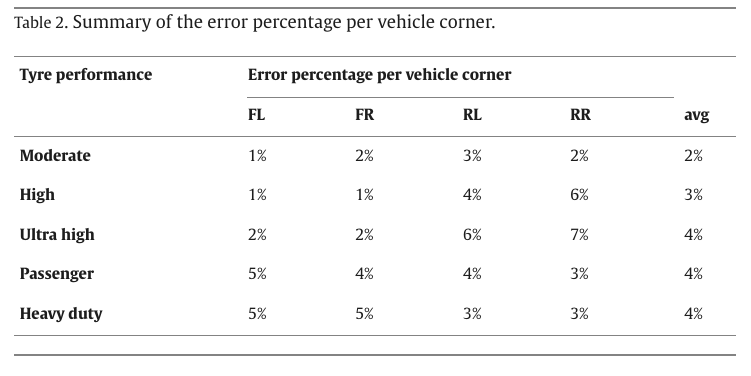
It can be seen from the collected wear observations and the simulated wear channels, available per rib, that the removal rates of a tyre tread compound are generally non-linear with running distance. In terms of final wear status, model results have been objectified by means of the normalized root mean square deviation percentage with respect to the experimental measures, for each tyre of the runs under analysis, and summarized in Table 2. Here it should be noted that, although there is no experimental information about how the final state is reached per each tyre spec, the proposed modelling approach appears quite accurate in predicting the final wear, returning error percentages of less than 5% in all cases.
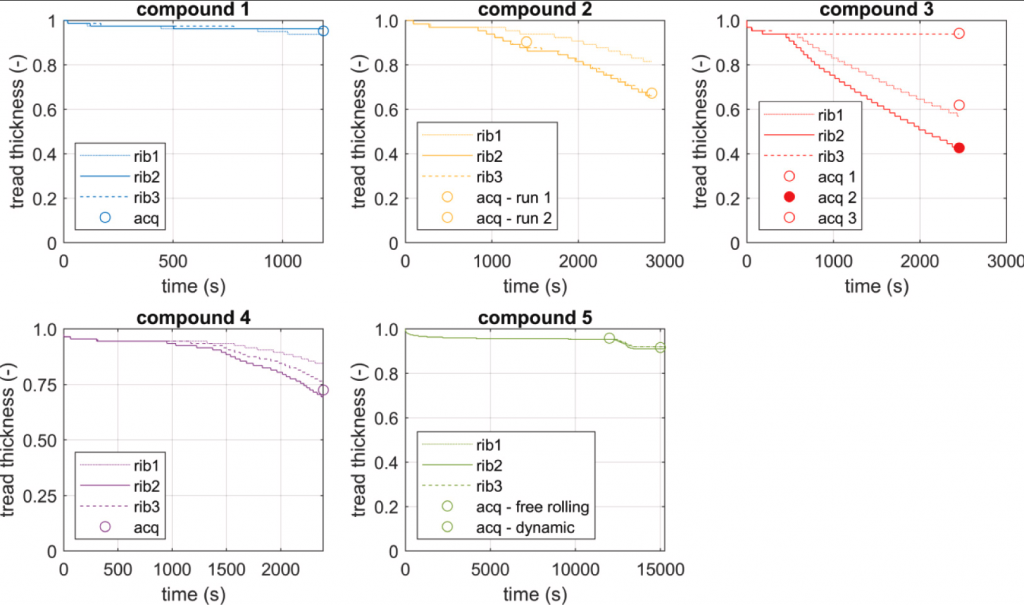
Fig. 12. Simulated and experimental tread wear comparison.
5. Conclusion
A simulation-oriented model for tyre wear quantification associated with the effect on friction coefficient generation and tyre thermal dynamics has been presented. A holistic approach that takes into account the multidisciplinary dependencies of the phenomenon has been adopted. More in detail, the contribution and mutual interactions of the tread compound viscoelastic properties, road roughness characteristics and wheel operating conditions within the contact patch have been all considered for an accurate wear calculation. Considering all these parameters as model input, the fatigue wear concept was extended as wear abrasion or simply wear. The proposed physical formulation has been validated experimentally by means of measurements from outdoor testing activities. In order to investigate the working range validity of the approach, five datasets for different applications have been selected. Results demonstrate the model’s reliability to reproduce the material removal for different tyres and in various thermal and dynamic operating conditions. For two of these compounds have been experimentally validated, not only the state of final wear but also the trend with the mileage by means of further measuring points. The model shows a non-linear trend evolution of the tread thickness.
From a practical point of view, the proposed model advantages embrace the capability to adapt to any simulation environment from ultra-detailed FEA co-simulation scenario up to a discrete single contact approach, where local temperature, contact pressure and velocity distributions and average values for the same quantities can be adopted, respectively. Indeed, the proposed formulation is suitable to work with both tyre global (assuming to have the instantaneous information concerning the contact patch area) and contact patch local quantities, enabling the possibility to be interfaced with both the real-time driver-in-the-loop simulators and the discretized numerical models based on finite element analysis. Moreover, the results from the conducted study in terms of reduced tread thickness, or removed rubber mass, can be exploited to feed advanced tyre dynamic models. For the sake of completeness, it has also to be pointed out that the current formulation does not take into account the degradation effect, linkable to the thermo-mechanical and chemical fatigue, on the viscoelastic and diffusivity properties of the compound. It is really a rough matter to discern different contributions to the performance decrease as a consequence of deeply interconnected phenomena both from the tribological and thermo-mechanical points of view. Therefore, these effects will be first specifically isolated and investigated in the laboratory-controlled environment.
CRediT authorship contribution statement
Aleksandr Sakhnevych: Conceptualization, Methodology, Writing – original draft. Andrea Genovese: Data curation, Investigation, Writing – review & editing.
Declaration of competing interest
The authors declare the following financial interests/personal relationships which may be considered as potential competing interests: Aleksandr Sakhnevych reports equipment, drugs, or supplies was provided by University of Naples Federico II. Aleksandr Sakhnevych reports a relationship with University of Naples Federico II that includes: employment.
Acknowledgements
We would like to express our sincere gratitude to the technicians Gennaro Stingo and Giuseppe Iovino of the University of Naples Federico II for their invaluable technical support throughout this project. We also extend our thanks to MegaRide and VESevo companies for providing the necessary resources and data acquisition tools that made this research possible. Their collaboration and support were crucial to achieving the objectives of this study, and their expertise and dedication have been essential in carrying out the experimental work and data analysis. We are grateful for their contributions and the opportunity to work together towards advancing the field of tribology.
Funding
No specific grant from any funding source in the public, commercial, or not-for-profit sectors has been involved in this research.