Tire Thermal Model – Abstract
Vehicle performances, especially in motorsport, are deeply affected by tire behavior and in particular by tire compound proper working conditions. In this research activity, a series of innovations have been introduced on the Thermo Racing Tire (a physical-analytical tire thermal model, based on Fourier’s law of heat transfer applied to a three-dimensional domain) in order to take into account all the main aspects actively involved in the thermal behavior of the tire, as the presence of exhausted gases eventually impacting at the rear axle and the inhomogeneous distribution of local variables (pressure, stress and sliding velocity) within the contact patch, caused in example by the tire camber angle.
The new model developed considers the presence of the sidewalls, actively involved in the convective heat exchanges, respectively, with the external airflow and the inner gas fluid, located inside the inflation chamber. The aim of the new version of the tire thermal model is a better physical comprehension of all the phenomena concerning the contact with the asphalt and the prediction of the link between the thermal state and the frictional performance, crucial for the definition of an optimal wheel and vehicle setup.
Introduction – Tire Thermal Model
In motorsport competitions, the test limitations imposed by race organizers rules or by budget restrictions have as a consequence the development of simulators to help drivers and technicians to prepare for upcoming events devising the vehicle setup.1
To this aim, it is necessary to have a detailed description of circuit characteristics, such as its geometry, bumps and kerbs shape and location, directly linked to the downforce levels, braking duty, and tire loads reachable under the defined setup conditions. The teams generally run a large amount of laps in the simulators, programmed with a variety of variables such as fuel loads and grip levels, to ensure as many scenarios as possible to be covered and to analyze as many race outcomes as possible.2,3
Engineering advances in sensor technologies during the last years allowed to introduce sensing elements even inside the wheel. The bigger volume of data collected during both tests and races to be processed met the availability of the reliable and predictive physical models, able to tune the vehicle and its components for optimum performance.
In this paper, a new physical tire thermal model (Thermo Racing Tire evolved (TRT EVO)) is developed starting from TRT thermodynamic model,4 according to the new simulation needs. Indeed, in addition to the temperature distributions within the tire layers, the influence of a large amount of parameters has been evaluated, among them: wheel alignments (as camber or toe), inflation pressure, the management of exhausted gases impact on the tires, different track and weather conditions, and the influence of the manufacturer’s vehicle settings.
To exploit the entire amount of grip available on the tire–road interface in order to preserve the highest level of handling performance preventing the tire from sliding, more and more physical phenomena regarding the vehicle and its subcomponents have to be taken into account within the integrated vehicle control systems.5,6 Tire characteristics in terms of braking and cornering stiffness and maximum amount of grip at various wheel operating conditions depend on an enormous number of parameters, among which are the tire compound core and sidewall temperatures, which modify the inner chamber air pressure,7,8 and the tire mechanical structure characteristics,9 as shown in Figure 1.
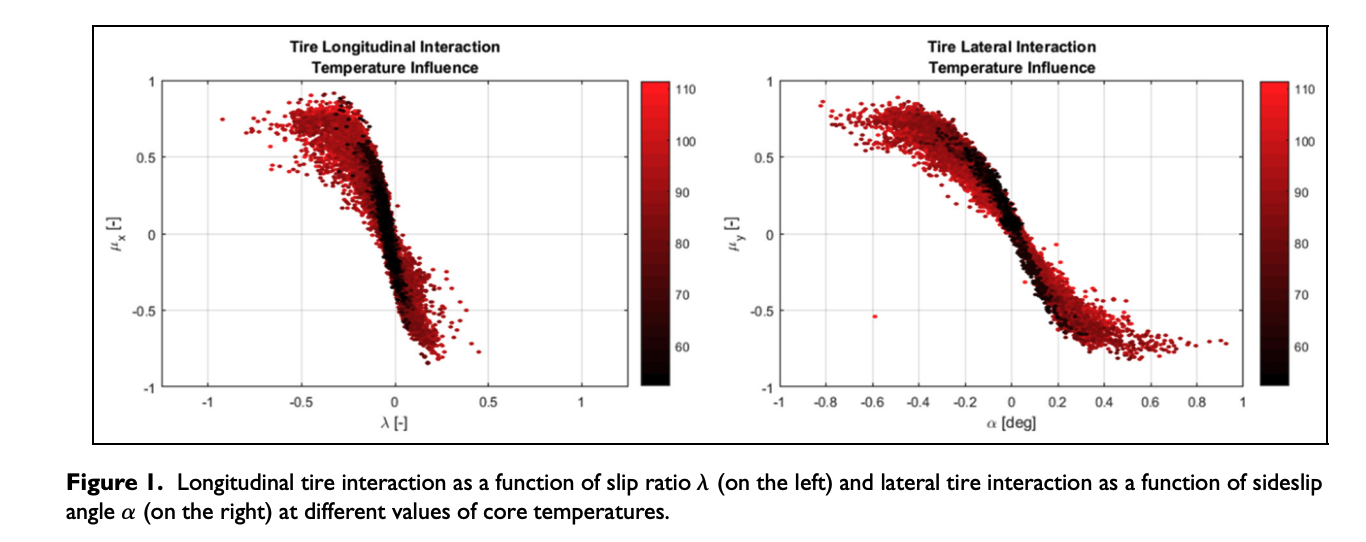
Differences in terms of interaction curves, highlighting a stiffness decrease due to a higher tire temperature, are shown both for longitudinal and for lateral tire interaction curves. The data represented have been nondimensionalized due to confidentiality agreements with the motorsport research partner.
The knowledge of the optimal temperature range for a generic tire compound is particularly significant in motorsport, being racing tires highly affected by thermal conditions of the tread and of the carcass structure. The relationship between the temperature of the bulk of the tread layer and the friction exhibited at road interface is usually described by a bell-shaped curve (Figure 2). The determination of the optimal working temperature of a tire in order to get its maximum grip is one of the key information for tire makers and motorsport team. Also, braking and cornering stiffness are highly affected by temperature (Figure 1), with particular reference to the temperatures of internal layers, linked to the structural variations and consequently to stiffness modifications.
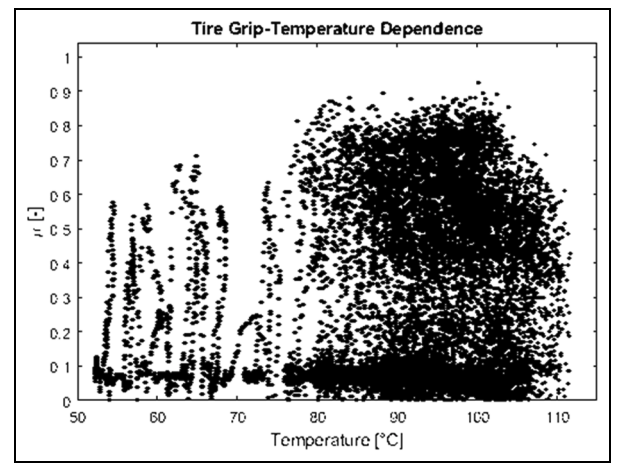
The availability of the thread bulk temperature (one of the cited internal layers, not obviously measurable) provided as an output by the real-time thermal model described in this paper, provide interesting correlations, which allow quite easily to identify the optimal thermal range.
The tire external surface temperature varies with an extremely fast dynamics, which clearly is bad correlated with the grip variation (which does not show a fast dynamics) this means that the surface temperature is not able to modify in so short time the whole tread mechanical characteristics. The grip shows an excellent correlation with tread internal temperature (this layer shows a slower dynamics of the same trend of the grip).
So the tire frictional behavior can be more realistically associated with the tread core layer temperature which can be used to optimize the compound mechanical characteristics starting from its thermal behavior; this temperature can only be evaluated by means of a specific tire thermal model.
The TRT model4 has been the basis of a the new model presented in this paper, built adopting an innovative simplified tire configuration and implementing a new structure of elements in order to obtain a complete tire temperature distribution in all the parts of the tire and in all the tire-working conditions.10 The latest upgrades have led to fit closer the response of the model to the telemetry data, minimizing, at the same time, the computational load.
At the current stage, additional boundary conditions concerning a wider range of tire-working conditions have been contemplated with the aim to extend the versatility of the new model. These include both the specific aerodynamic solutions adopted by the car designers and the different wheel alignment configurations studied in order to optimize the performance of the vehicle in each peculiar track. The inhomogeneous distributions of local variables have been contemplated employing methodologies able to not increase the computational burden of the model, guaranteeing real-time simulations.
So the TRT EVO model constitutes a development tool useful to study and understand all the thermal phenomena concerning the tire during its interaction with both the external environment and the internal air.
TRT EVO model
In the TRT model,4 only the tread and the layers underlying it were considered. The tire structure was lacking of sidewalls and so the model was not able to reproduce the temperature distribution in all the parts of the system, losing important elements influencing the tire behavior. In any case, the availability of the bulk temperature in the TRT allowed to identify the compound optimal thermal range,11 starting from the polymer thermal characteristics, appropriately evaluated by means of indoor test procedures and a specifically developed version of the model for laboratory activities (TRT LAB).12,13
Modeling assumptions
The TRT EVO model is mainly designed to take into account the main physical phenomena, able to influence tire thermal dynamics. The radiation heat mechanism is supposed to be negligible, so the tire system that exchanges with the external environment can be properly described by convective and conductive terms.
The TRT EVO is a physical-analytical model based on Fourier’s law conceived in the Lagrangian reference system. The tire is considered motionless and the boundary conditions, linked with external environment thermal exchanges, vary during the simulation.
The road is schematized as a geometric homogeneous even plane, in contact with the tire portion corresponding to the contact patch under a particular load condition. The remaining tire surface is involved in the convective heat exchange with the external air, whose entity is determined by means of specific computational fluid dynamics (CFD) analysis, on whose basis interpolative analytical functions are identified to guarantee the real-time attitude. The road temperature Tr and the air temperature Tair influence the boundary conditions of the model, taking into account the track weather conditions.
The tire contact area is assumed to be rectangular in shape. Its dimensions, width W and length La, depend on the tire structural radial stiffness and are function of the vertical load Fz, of the inner pressure pin, and of the camber angle γ, on the basis of the results of specifically developed testing procedures, based on the pressure sensitive films.14 The influence of the toe angle φ over the contact patch shape has not been taken into account.
Tire discretization
A tire is an extremely complex and integrated system,15 whose structure can be arranged in three layers, each serving diversiform functions:
•Tread compound is accountable for the generation of tangential interaction forces within the contact patch extension;
•Body plies, belts, and sidewalls determine the carcass shape and the contact patch configuration, thus defining the tire interaction;
•Innerliner layer maintains the inflation pressure.
Tires vary considerably their behavior with temperature and excitation frequency,16 in particular as concerns the tread viscoelastic layer behavior and its effect on tire grip. On the contrary, the temperatures of the internal tire layers and of the sidewalls influence the tire cornering stiffness, establishing a connection between the tire temperature and the entire vehicle handling characteristics17,18
After a proper evaluation, the least computationally expensive solution to take into account the tire high inhomogeneity has resulted in the adoption of a thermal equivalent dual-zone material configuration along the radial direction: the tread constituted only by rubber compound and the carcass composite structure, including belt and innerliner, as represented in Figure 3.
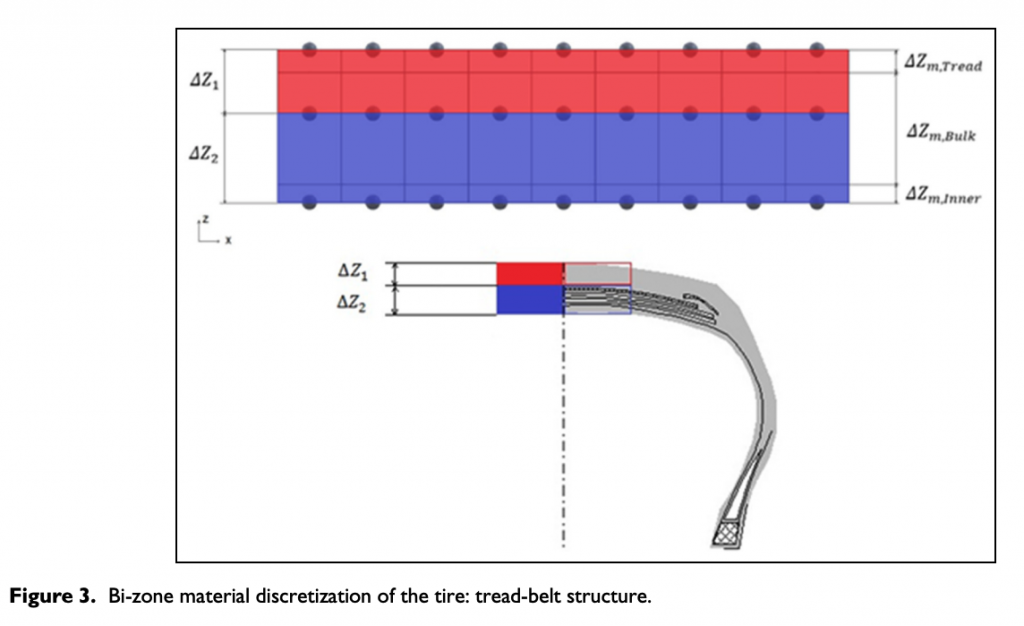
This peculiar parting is adopted in order to study and analyze singularly the tread ΔZ1 and the reinforcement composite ΔZ2 zones. The tire is considered lacking of grooves (slick) and unrolled, forming a heterogeneous parallelepiped.
As concerns the thermal inertial properties, the entire tire thickness is subdivided into three grid layers along the radial direction z, whose nodes represent the points in which the temperature is evaluated. Particular attention has been focused on the definition of the terms ΔZm,Tread, ΔZm,Bulk, and ΔZm,Inner, as shown in Figure 3, directly connected to the thermal inertias of different tire strata, whose values can be evaluated through a specifically developed test procedure, accurately described Farroni et al.10 The subscript m stands for the fact that ΔZm,Tread, ΔZm,Bulk, and ΔZm,Inner regard the radial mass dimension of the individuated tire layers, useful to model the thermal transient phenomena as the flash temperature on the tread surface19,20 and the convective heat exchange at the innerliner internal boundary (while ΔZ1 and ΔZ2 concern the thermal and mechanical material characteristics of the above-mentioned zones).
Each layer is discretized by means of grid of nodes to each of whom a thermal inertia term, expressed as a parallelepiped volume Vi, is associated

where the quantities Δx and Δy represent the dimensions of the parallelepiped along the longitudinal-circumferential and the transversal-wide tire directions.
Thermodynamic equations
The developed thermodynamic tire model is based on the use of the diffusion equation of Fourier applied to a three-dimensional domain.
The complexity of the transient thermodynamic phenomena under study and the degree of accuracy required imply the dependence of the thermodynamic quantities, and in particular of the thermal diffusivity terms, on the temperature. Furthermore, the non-homogeneity of the tire has made it necessary to consider the variation of the above parameter also along the thickness.
Therefore, the Fourier equation takes the following formulation applied to a considered three-dimensional heterogeneous domain
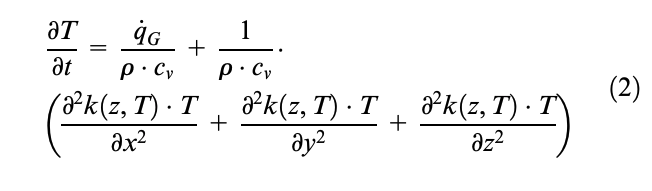
Writing the power balance equations for each elementary mass associated with each node, in relation to its position within the tire structure, the matrix equation of the entire model can be obtained in the typical state form4
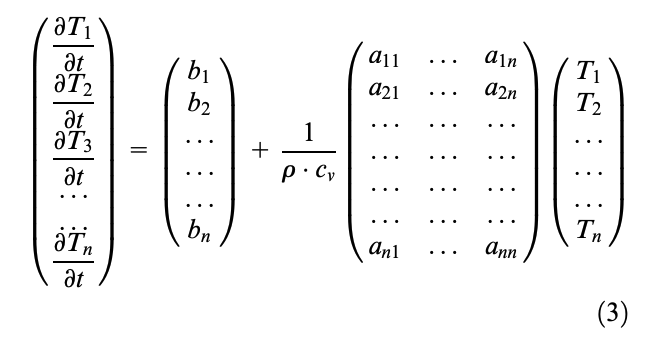
The input data for the TRT EVO model consist of the following telemetry channels: normal, longitudinal and lateral tire–road interaction forces, longitudinal and lateral sliding speeds, forward speed at the wheel hub center, and the boundary weather conditions as air and road temperatures.
Each tire is characterized both by its structural characteristics and by its peculiar thermal properties so that a specific set of physical parameters has to be identified to properly describe the tire thermo-inertial behavior.12,13 The thermal diffusivity of the track pavement has been preliminarily analyzed for different tracks to accurately model the heat exchanges associated with the tire–road conduction term.
Considering the tire as a thermo-mechanical system, as already described in Farroni and colleagues,4,10 in addition to the conductive mechanisms within the composite structure due to the temperature gradients, the following heat transfer mechanisms have been taken into account:
•Heat generation terms connected with the friction phenomena arising at the interface with the asphalt pavement and the stress-deformation cycles of the whole tire mass during the operation:
•Tire–road longitudinal–lateral interaction generation, known as “FP” (friction power), concerning the contact patch extension and directly connected with thermal powers as a function of global tangential interaction forces and the relative sliding velocities between the tire surface and the uneven asphalt;
•Effect of tire cyclic deformation and recovery, known as “SEL” (strain energy loss), associated with the tire rolling resistance and the operating phases with significant values of interaction forces and, thus, structural internal deformations;
•Heat exchange with the external environment (as said the radiation mechanism is neglected by hypothesis) due to:
•Thermal conduction between the tire tread and the road pavement, as a function of the compound thermal characteristics;
•Forced convection of the surface layer with the outside air and of the innerliner surface with the inner gas, both described by Newton’s law of cooling, whose magnitude is dependent on the value of the relative velocity of surface nodes and air flux, evaluated by means of CFD simulations.21,22
The TRT EVO model is able, by means of tread subdivision in ribs, to describe the inhomogeneous distributions of local variables within the contact patch, as stresses or deformations due to specific working conditions of the wheel and thus of the tire. This has become necessary to study different suspensions solutions, characterized by different wheel alignment angles and contact patch shapes and extensions.
So the model allows to study the effects of different vehicle setup (camber and toe angles or inflation pressures), in order to enhance the tire response in the widest possible range of working conditions. The above distributions have been modeled varying in each rib the thermal powers and the cooling terms due to tire–road interaction as a function of the described parameters.
Development of new features
The computational burden, connected with the number of the state variables and therefore of the equations considered, has been reduced substituting the node grid configuration of the tire inner layers (bulk and innerliner) with a singular node configuration, as represented in Figure 4.10 Consequently, the number of nodes has been reduced from n to (n/3 + 2), considering a singular rib configuration, assigning the same thermal intrinsic characteristics (density ρ, specific heat cv, and conductivity K). So to simplify the discretization the tire, entire internal grid layers have been condensed to singular nodes, because their thermal inertias, even within a very fast vehicle dynamics, are too ponderous to induce a significant temperature circumferential gradient.
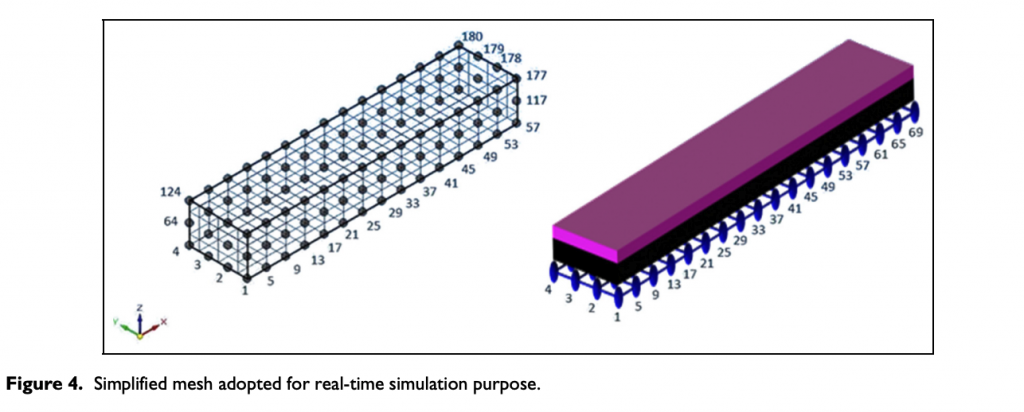
The surface layer is still modeled by means of a grid of nodes, whereas a singular node configuration has been adopted for the internal tire layers: bulk (intermediate parallelepiped in black in Figure 4) and innerliner (in magenta). Thus, the volumes attributed to the inner coatings, taking into account the global tire dimensions, as tire unrolled length La and width W, can be expressed as follows

With this simplification, the TRT EVO model is able to consider also the sidewalls within the tire physical structure and a further discretization along the circumferential direction within the external layer to reproduce more accurately the particularly fast thermal dynamics of the tire surface without undermining the simulation real-time requirement.
Consequently, the tangential heat exchanges of the internal tire nodes have been neglected and only the radial conduction has been considered. Assuming the contour of bulk and innerliner nodes as unrolled parallelepipeds, the area affected by the radial heat exchange is rectangle, whose dimensions correspond to the tire width and circumferential length. Consequently, the heat balance equations are as follows
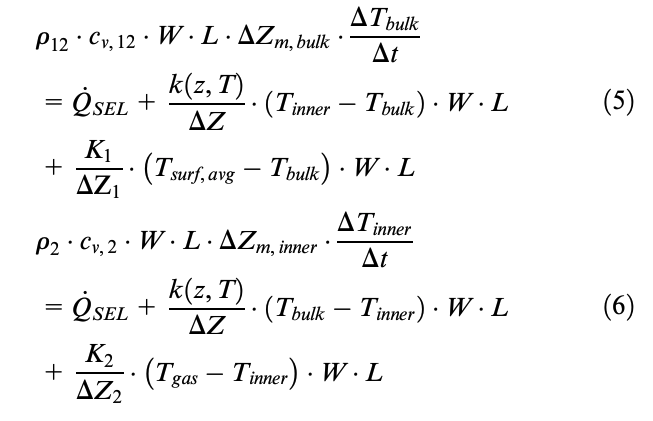
where Tsurf,avg is the average grid temperature value of the tire surface layer. The equations are then specifically developed in normal form (equations (7) and (8)) as follows
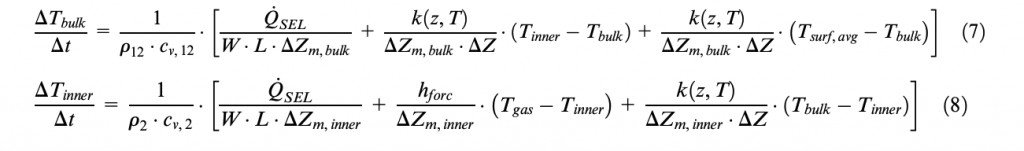
During rolling, tires are subject to periodic deformations, inducing time-dependent load history on the tire system, which causes temperature arise inside the tire structure because of both elastic-viscous mechanical characteristics and a low thermal diffusivity. The modeling of tire sidewalls, actively involved in the convective heat exchanges with inner and outer air fluxes and subject to fatigue induced by tire–road interaction, is evidently necessary to understand the thermal aspects related to optimal operation purpose and long service life.23,24
Including the sidewalls within the tire structure allows to get a more detailed physical representation of the whole wheel chamber, providing an instrument to study and understand the effects of the inner gas dynamics on the thermo-mechanical behavior of the tire. Moreover, a large fraction of SEL is dissipated inside the sidewalls because of their large deformations.
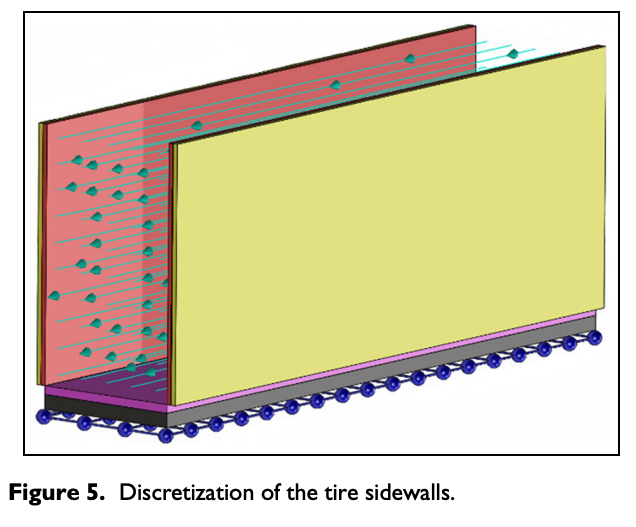
As shown in Figure 5, the implemented sidewalls have been discretized, each by means of two parallelepiped nodes, whose dimensions are as follows: the tire unrolled length considering the average radius value, sidewall height, and half of the sidewall medium thickness, since the sidewall section is really irregular within the meridian reference plane.
In particular, the above measures have been calculated knowing the tire geometry, thus obtaining the heat transfer area ASide. The sidewall nodes, called surface (in yellow) and bulk (in red), are, respectively, in contact with the external air flux and with the inner gas contained inside the wheel chamber. In order to properly describe the heat conduction phenomena, the entire discretized volume has to be physically characterized, evaluating the material thermal and inertial properties.12,13
The heat balance equations related to the bi-node configuration of each tire sidewall are as follows
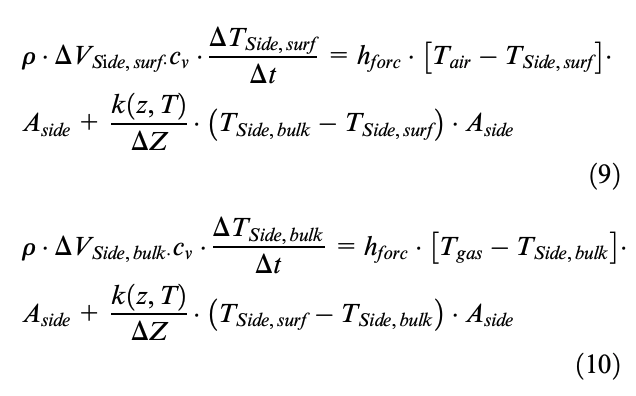
Equations (9) and (10) are further developed as follows
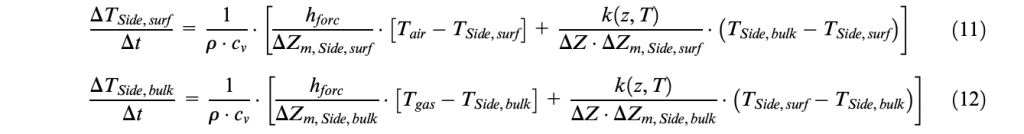
It is important to highlight that the evaluation of the thermal diffusivity is particularly delicate due to its intrinsic dependence on the temperature and a wide range of complex tire structures.25
Implementation of particular boundary conditions
The TRT EVO structure has allowed the implementation of features required for particular applications, as the presence of additional heating sources due to the hot gases investing tires in localized spots, or the discretization of the tread along its lateral direction, useful to take into account under/over-inflation conditions and the modeling of the interaction with road under high camber angles.
The obtained results laid the foundation for further developments, leading to the creation of a motorcycle version of the tire thermal model, object of a next stage of the research activities.
Hot gas on tires from exhaust blown aero diffusers
The vehicle rear end is able to create downforce by means of two different elements: rear wings and diffusers. The optimal solution would consist in linking them together to create the best amount of downforce with minimum drag.
The engine exhaust gases have been used in several cases in motorsport with the aim to increase the air flux passing through the diffusers, enhancing the downforce. Besides being used for aerodynamic purposes, the exhaust gases can be also used to provide further heat in case of need for the achievement of the optimal working temperature, around the tires. The thermal contribution coming from the exhaust gases, directed to the rear of the car, deeply depends on the aerodynamic geometry adopted and it can be specifically designed to invest different areas of the tires.
If improperly canalized, the additional thermal sources risk to damage the tire because of too high thermal stress levels induced. So, each adopted solution has to be studied in detail in order to properly handle the supplementary heat flow, whose correct employment may represent a key factor for the management of the tires in terms of optimization of the grip/temperature relationship during particular operating phases.11–13
The extremely severe thermal conditions due to localized hot gas flows have been modeled inside the TRT EVO model taking into consideration an external localized thermal source. The tire is considered motionless and the boundary conditions move, varying by means of specific permutation matrices, function of the wheel angular velocity. In addition to the convective and generative thermal terms, the tire is subjected to the additional heat convection at specific points of the tire external layer hit with the exhaust gases.
To take into account the effect of the exhaust blown gas, the external tire surface not in contact with the road, including tread and sidewalls, has been accordingly divided into two zones: one affected by the convective external cooling airflow and the other one warmed by the exhaust gas impact (Figure 6).

The information, in terms of the number of nodes interested by the exhaust gas warming effect and their position within the surface layer grid, is a function of the particular exhaust system adopted and it is assigned in pre-processing.
The convection heat transfer term, concerning the exhaust gas flow, is expressed by Newton’s law of cooling
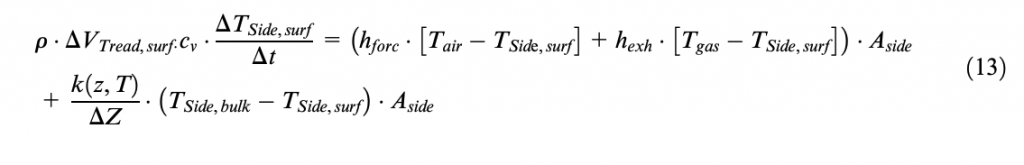
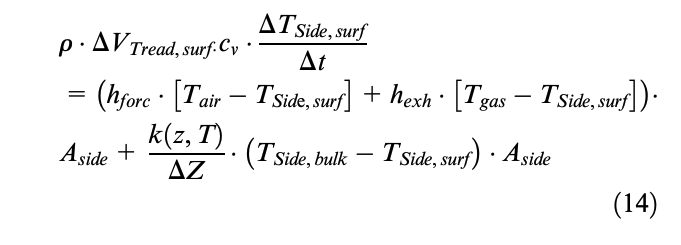
Development of multi-ribbed contact patch
One of the main limits of the TRT4 is definitely due to the fact that is based on global quantities, which are not able to describe the inhomogeneous distribution of local variables inside the contact patch, for example, stresses and deformations due to camber thrust. In particular, the model has as an input the forces and sliding velocities that the tire globally exchanges with the road.
TRT EVO ribs modeling allows to study the effects linked with the most common tire configurations, like nonzero camber angles and/or under/over-inflation. At present stage, the model includes five ribs and six knots in the lateral direction, as represented in Figure 7. To determine the amount of the FP per each rib, it becomes necessary to provide different local forces and sliding velocities, evaluated, for example, by means of specific contact models.26,27
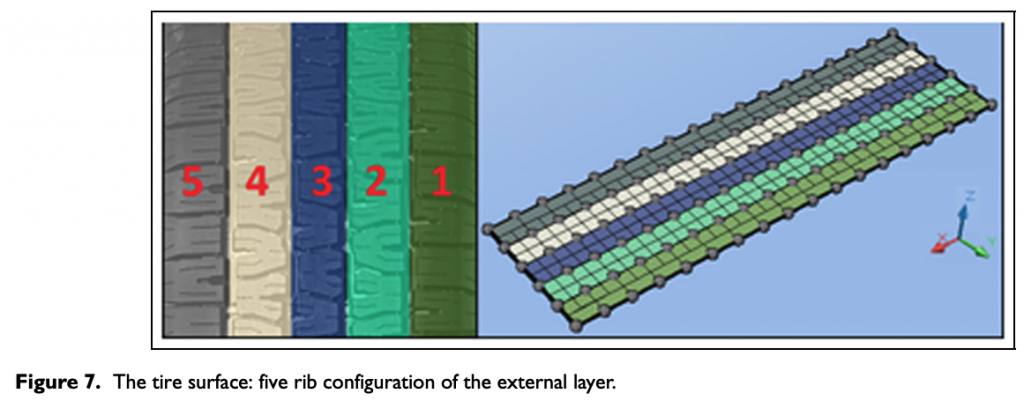
Moreover, per each rib, TRT EVO provides the possibility to diversify both the thermal power terms and the material mechanical/thermal properties. This allows to evaluate the temperature distribution within the whole tire: both inside the contact patch taking into account the distribution due to camber thrust and/or under/over-inflation tire condition and as concerns the part of tread in contact with the external airflow influenced by specific aerodynamic solutions.
Each single rib is characterized by a specific value of thermal diffusivity depending on its temperature. A node completely belonging to a single rib is characterized by an FP value calculated on the basis of forces and velocities assigned to the rib by the contact model; physical quantities relative to nodes localized between two consecutive ribs have been considered as the mean value of the ones assigned them.
A single rib is therefore identified by two stripes of nodes along the x direction so that all the lines are subjected to the heat exchanges concerning the ribs they belong to. Finally, considering the nodes belonging to rib 5 (in gray in Figure 7), the heat balance equations related to, respectively, the surface layer’s external and internal nodes are as follows
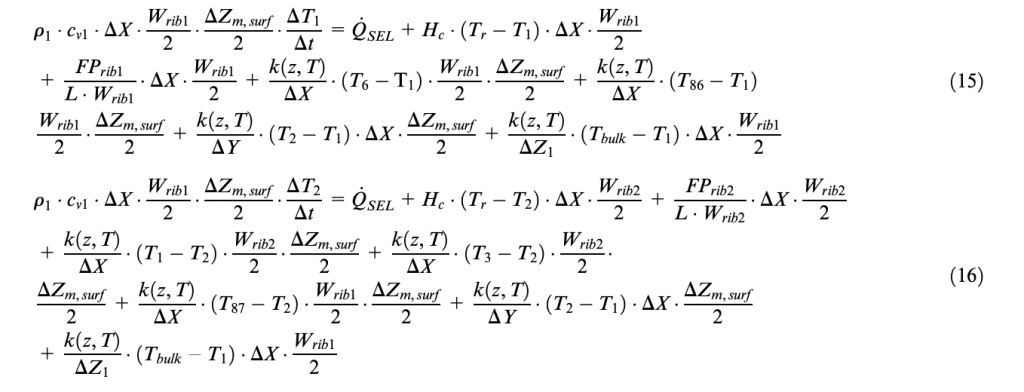
Equations (15) and (16) are further developed as follows
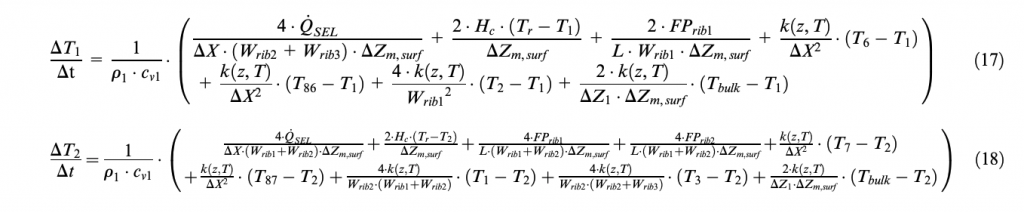
TRT EVO can be usefully employed to reproduce the behavior of a common ribbed passenger tire, subdividing it in a certain number of homogeneous zones not interacting each other within the surface layer.
In this case, the singular ribs are involved in conductive heat transfer only with the bulk layer along the radial direction of the tire. Neglecting the heat transfer phenomenon between the different ribs along the lateral direction, the heat balance equations therefore become the following

Equations (19) and (20) are further developed as follows
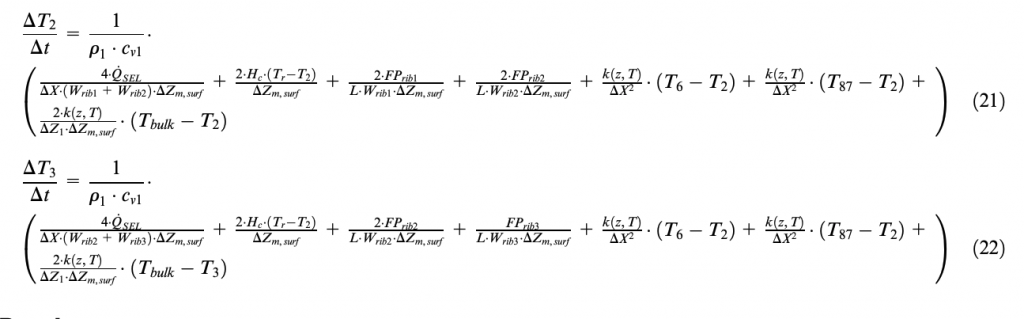
Results
In order to compare properly the original fully discretized TRT model4 and the optimized mononode conceived TRT EVO, only the three layers have been considered within the TRT EVO tire structure, neglecting the presence of sidewalls in thermal exchanges. A comparison between the temperature distributions within the whole tire obtained, respectively, by means of the original TRT model4 and the optimized TRT EVO is illustrated in Figure 8. With the same set of initial and boundary conditions, the models differ in less than 1°C after a 550 s simulation that is a rather good compromise between both aspects: real-time simulation target with lower computational load and full analytical model.
Because of confidentiality, the temperature values are nondimensional in all figures, with reference to the maximum temperature value reached during the simulations carried out.
Adopting the TRT EVO mononode model configuration and implementing the sidewall nodes within the tire structure, the thermal system consisting of the whole wheel can be finally studied. The temperature air inside the wheel chamber, rim temperature, and different cooling solutions can be thus properly analyzed to choose the best solution to optimize the compound behavior,6 since their position toward the longitudinal reference tire plane, the internal and external sidewalls can differ significantly in terms of stress/deformation and thus of heat generation and thermal exchanges.
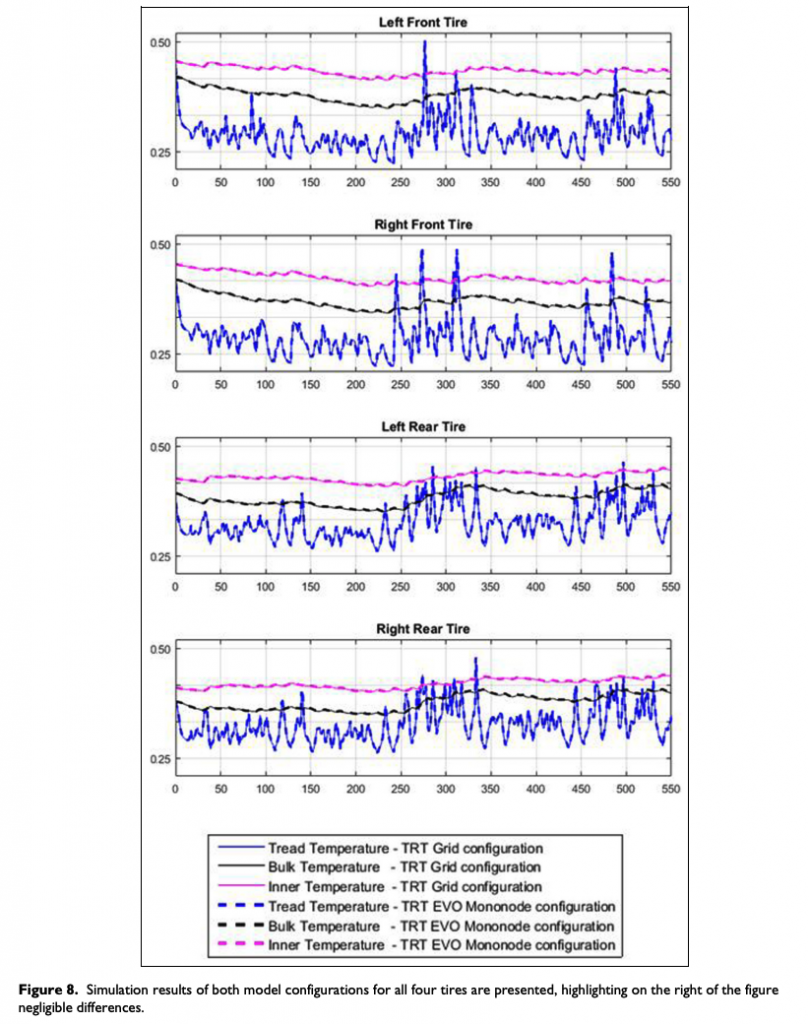
The temperature trends of all the nodes considered within the TRT EVO tire structure are represented in Figure 9 for a run on a reference track.
In Figure 9, it is possible to compare qualitatively the thermal trends of the nodes belonging to, respectively, the tire internal (bulk) and external (surface) sidewall layers and to observe the different dynamics of the surface, bulk and innerliner layers due to the described interactions with the external environment. In particular, it is possible to highlight the very fast thermal dynamics of the tire tread due to the FP heating and the forced convection cooling.
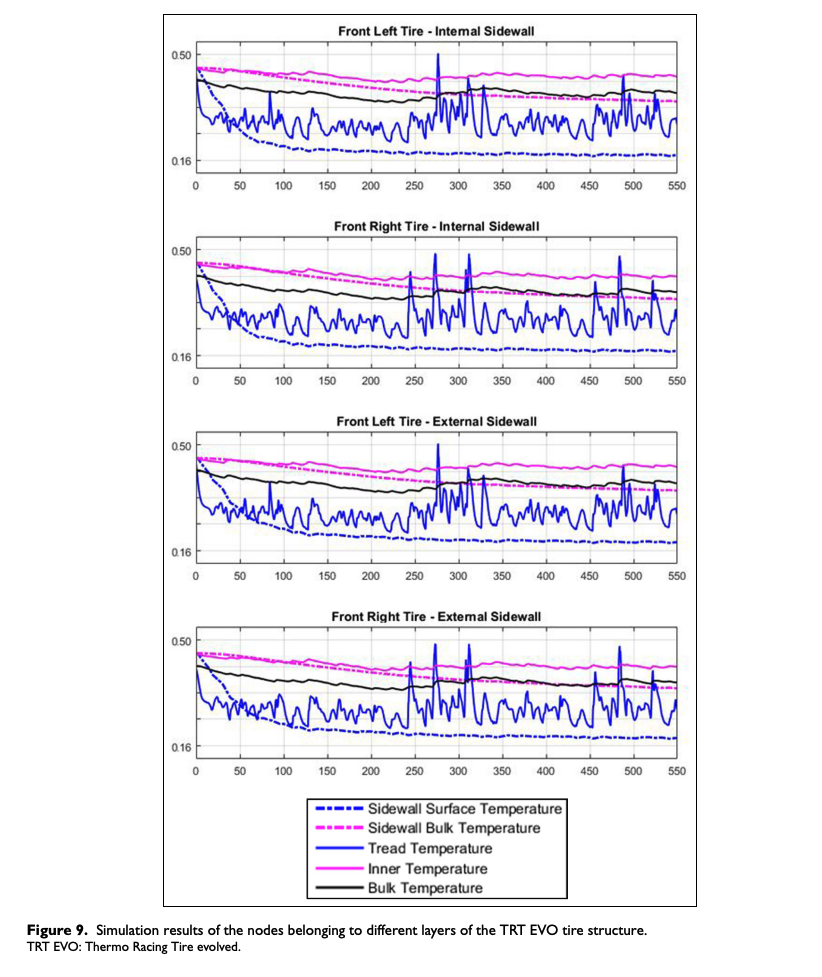
As concerns the tire temperature analysis of the rear vehicle axle, it has been possible to evaluate the effect of the exhaust gases flow impact on a portion of the tire external layer by means of TRT EVO model. The results, reported in Figure 10, show that the tire temperature distribution can be strongly modified, both on the external and on the internal tire layers, adopting an appropriate aerodynamic solution.
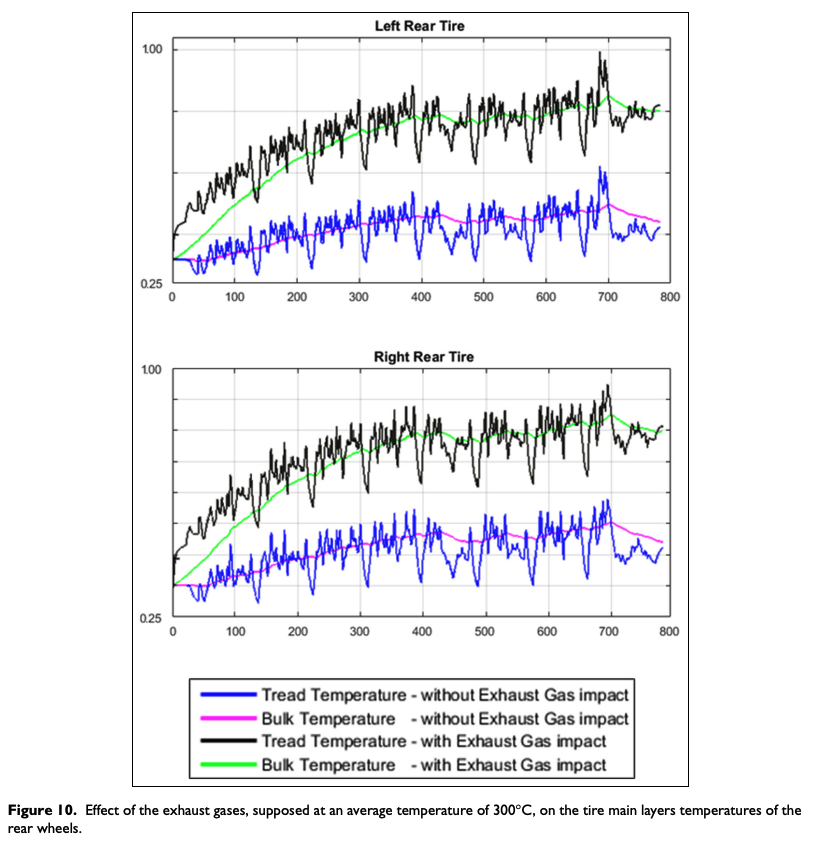
In this case, assuming that the average temperature of the exhaust gas is equal to 300°C, Figure 10 puts into evidence the relevance of the phenomenon both in steady state and in transient conditions for the rear tires. These temperature differences may result in diversification of response in terms of tire performance regarding both the compound viscoelastic characteristics and the carcass thermo-mechanical behavior. The first one is connected to the tread temperature and thus to the friction level arising at the tire–road interface, meanwhile the second one is linked to the temperatures of tire bulk and sidewalls.11
To examine the described issue in depth and to carry out more accurate estimations of exhaust gas heating at the rear axle, TRT EVO model is able to take also into account the following:
•A precise formulation of the convective heat transfer coefficient hexh as a function of the instantaneous thermo-physical properties of the exhaust gases and of the mutual velocity between the flow and the external tire layer;
•A real measure of the gases temperature and their accurate distribution in the impact zone;
•A proper estimation of the heating phenomenon concerning the rear tire sidewalls.
As concerns the TRT EVO model with the rib implementation, in order to provide a detailed results analysis, both the average temperature time histories per rib and the spatial temperature distribution are presented in Figure 11, where the particular enumerating adopted is described in Figure 7.
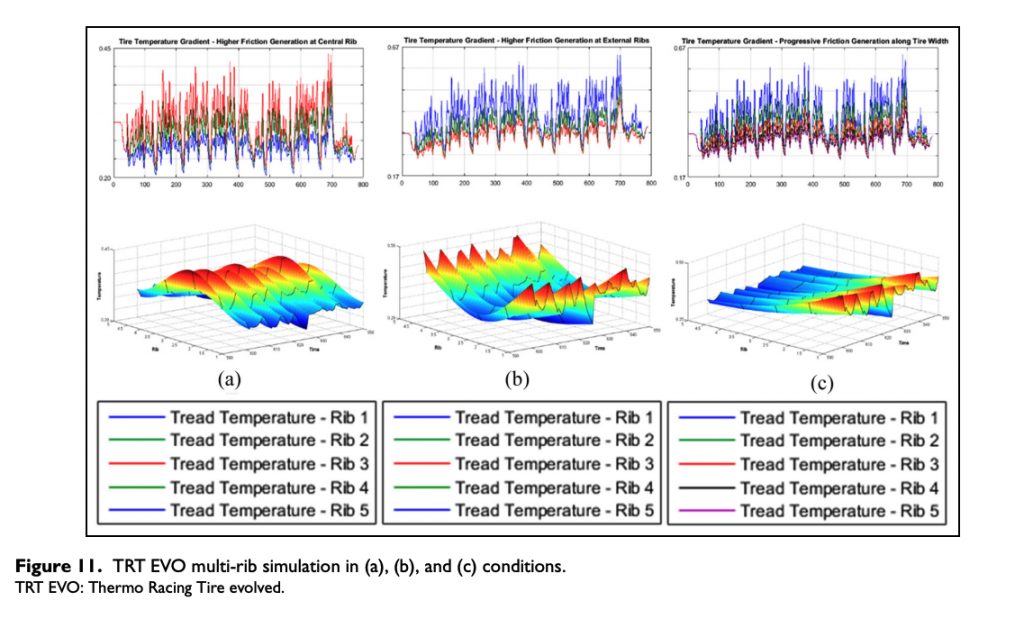
Hypothesizing the ribs masses being equal, with the aim to evaluate the model response in the widest possible range of tire operating conditions, three main configurations have been analyzed. In Figure 11, three different conditions of the heating FP distribution along the lateral direction have been assigned to the tread pattern at the tire–road interface:
a. A maximum FP value assigned to the central rib 3, equal up to four times the heat rate affecting the remaining ribs. This warming situation is characteristic of tire behavior contact patch in over-inflation conditions;
b. A maximum FP value assigned to the external ribs 1 and 5, which reproduces tire behavior contact patch in under-inflation conditions;
c. An FP gradient distribution along the tire lateral direction, simulating the presence of camber thrust in a generic operating condition.
In the absence of wheel alignment angles, supplying the heating rate only to a central rib (Figure 11(a)), a symmetrical temperature distribution is obtained toward the longitudinal tire plane. The tread temperatures of ribs 1 and 5 and of 2 and 4 are characterized by the same trend throughout the entire simulation, with maximum temperature value at the central one.
In the absence of wheel alignment angles, supplying the heating rate only to the external ribs (Figure 11(b)), a symmetrical temperature distribution is obtained toward the longitudinal tire plane. The tread temperatures of ribs 1 and 5 and in the same way of the 2 and 4 are coincident, with maximum temperature values at the external ones.
In the presence of wheel alignment angles as camber thrust (Figure 11(c)), the heating rate is supplied to the tire contact pattern as FP gradient with maximum value at rib 1. The tread temperatures of all ribs are diverse throughout the entire simulation, with maximum temperature value at rib 1 and minimum one at rib 5.
It is clear how the ribs, operating under heavier thermal conditions, reach higher temperature values, confirming the validity of the described implementations. The described quantitative analysis, in terms of average temperatures of the surface ribs, provided by means of the TRT EVO model, can be used to properly set the air pressure inside the wheel chamber with particular attention to the tire durability and the performance gain obtainable due to the temperature dependence concerning the viscoelastic tread compound behavior.
Conclusion – Tire Thermal Model
In the present paper, an innovative tire thermal model called TRT EVO has been presented, able to take into account the warming effect of the exhaust gases as well as the thermal effect due to the sidewall presence, to wheel alignment angles and to inflation pressure.
The adoption of an innovative simplified tire configuration and the implementation of a specific mesh allowed to obtain a multipurpose analysis instrument able to reproduce the thermal dynamics of the tire in almost all the most interesting operating conditions. Fitting the response of the model to the telemetry data and, at the same time, minimizing the expended computational resources, the presented TRT EVO model aims to provide a tool useful to study and understand completely all the thermal phenomena concerning the tire during its interaction with both the external environment and the internal inflation chamber within the wheel system. Indeed, the factors like the inflation pressure, and its influence on the tire thermomechanical behavior, the wheel alignment angles, and the aero vehicle configuration can be optimized with the above instrument.
The difference in the thermal dynamics of the diverse layers is due to their position within the tire composite structure: the tread is subjected to the generative terms connected to instant friction thermal power at the tire–road interface and thus its temperature profile is oscillating, whereas a slow temperature slope, induced concurrently by the rolling fatigue effect and by the convective heat exchanges, characterizes the sidewalls dynamics.
The next step in the tire thermal model development process would be the integration of the wear phenomenon to evaluate the effects of physical abrasion and chemical decay of the tire tread layer from the thermal point of view.
It has to be highlighted that, once per season, it is necessary to carry out an appropriate set of tuning factors to use it in a predictive manner. The above procedure is linked with the vehicle-specific configuration, connected with car setup and tires construction, allowing to adopt the model for analysis and supporting vehicle design determination.
Declaration of conflicting interests
The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Funding
The author(s) received no financial support for the research, authorship, and/or publication of this article.
ORCID iD
Flavio Farroni https://orcid.org/0000-0001-8257-5534
Appendix 1
Notation
A surface geometry of the structure nodes (m2)
cv specific heat of tire structure nodes (J/kg K)
FP thermal generative term due to friction power (W)
hforc convection transfer coefficient to reproduce air convection (W/m2 K)
Hc virtual convection coefficient to reproduce road conduction (W/m2 K)
K thermal conductivity of tire structure nodes (W/m K)
La tire tread unrolled length (m)
pin internal pressure (bar)
Qsel thermal generative term due to strain energy loss (W)
Ti temperature of ith node of the tire structure (K)
Tair temperature of the external air (K)
Troad temperature of the road pavement (K)
Tgas temperature of the additional exhaust thermal source (K)
W tire total tread width (m)
Wi tire tread ith rib width (m)
z radial direction of the model reference system (m)
α tire sideslip angle (deg)
ΔX circumferential dimension of the structure nodes (m)
ΔY lateral dimension of the structure nodes (m)
ΔZm,i radial dimension of ith node (m)
λ tire slip ratio (−)
ρ density of tire structure nodes (kg/m3)